(e)시대와 철학

『독일 이데올로기』1·2(2019), 『정신의 오디세이: 자유 의지의 역사』(2021) 등을 저술한 전 동아대 철학과 교수 이병창 회원이 영화와 소설, 철학 등 광범위한 문화 비평을 담아내는 코너이다.

헤겔 형이상학 산책55-미적분은 정당한가(4)[흐린 창가에서-이병창의 문화비평]

2025년 12월 20일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책55-미적분은 정당한가(4)

이상에서 헤겔은 뉴턴의 미분 증명이 이론적으로는 다른 미분 증명보다 탁월한 점을 제시했다. 그것은 페르마, 라이프니츠, 칸트 등이 여전히 무한소나, 사라지는 크기 개념에 매달렸을 때, 뉴턴은 최종 비례라는 개념에 도달했기 때문이다. 미분은 곧 최종 비례이다.

그런데 헤겔은 뉴턴이 이론적으로 확립한 이런 최종 비 개념이 실제 계산 과정에서는 무시되고 말았다고 말한다. 헤겔은 그 이유를 세 가지로 제시한다.

①계산을 편리하게 한다는 욕구가 미분 계산이 지닌 문제점을 간과하게 했다.

헤겔은 뉴턴이 범한 오류를 곱하기 즉 x*y의 미분을 끌어낸 증명에서 발견했다. 이 곱하기의 미분은 (x+1/2dx)(y+1/2dy)-(x+1/2dx)(y-1/2dy)이다. 뉴턴은 그 답이 xdy+ydx라고 했는데 사실은 dxdy가 추가돼야 한다.

그런데도 계산상의 욕구가 뉴턴이 자기 답이 오류라는 것을 무시하게 했다는 것이다. 헤겔에 따르면 뉴턴은 마찬가지로 미분 계산에서 첫 번째 항을 제외한 나머지 항은 그 값이 사소하기에 계산의 편의를 위해 버려도 무방하다고 보았다고 한다.

② 운동의 함수를 보면, 등속 운동은 v=ct 로 표현되고, 등가속 운동은 s=1/2at²이며 저항은 3차 함수로 표현된다. 그러므로 뉴턴은(이는 사실 라그랑쥬에서부터 유래하는데) 미분을 위한 전개식에서 첫 번째 항은 등속 운동을 의미하고, 두 번째 항은 등가속 운동, 세 번째 항은 저항을 의미한다고 본다. 이것은 전개식의 각 항에 질적 의미가 있다고 보는데, 예를 들어 낙하운동의 속도를 구하는 미분에서는 첫 번째 항 속도와 무관한 두 번째 이하의 항은 관계없으니 무의미한 것이라 보면서 제거했다는 것이다.

③세 번째는 카르노처럼 미분 계산에서 나오는 이항 정리에서 각 항은 동일한 비례가 반복되는 것에 불과하니, 버려도 된다는 주장이다.

이어서 헤겔은 라그랑쥬의 입장도 소개하는데, 그는 뉴턴에 귀속되는 이유 중 ②을 포함하여 새로운 이유를 갖는다고 한다. 그 이유는 다음과 같다. 즉 미분 계산 가운데 이항 전개에서 나오는 각 항은 그다음 모든 항의 합보다 크기 때문에 무시할 수 있다는 것이다. 왜냐하면, 항은 점차 미분의 거듭제곱이 더 커지는 것인데(예를 들어 dx, dx², dx³ …) dx가 아주 작은 수이니 그 제곱은 제곱으로 작아지기 때문이다. 라그랑주가 들고 있는 이 이유는 사실 첫 번째 항을 제외한 나머지 항은 그 값이 사소하다는 주장과 같은 주장이니 주장①에 통합해도 될 것이다.

라그랑쥬의 주장을 제쳐 놓으면, 남은 것은 뉴턴이 말한 세 가지 이유다. 이 가운데 ②, ③ 주장은 그 주장 자체가 합리적으로 이해되지 않는다. 상식적으로 그럴 것 같지 않은 주장이기 때문이다. 뉴턴이 정말 그랬을까 싶은데, 일단 헤겔은 그렇게 파악한다는 사실만 말하고자 한다. 헤겔 자신도 그런 주장을 소개만 할 뿐, 정당한지는 따로 말하지 않는다.

그러므로 핵심은 역시 첫 번째 주장에 있다. 뉴턴은 이론적으로는 최종 비례라는 개념을 끌어냈으나, 실제 계산에서는 다시 최종적 크기, 또는 사라지는 크기라는 개념으로 되돌아가면서, 라이프니츠와 마찬가지로 나머지 항은 크기가 작으므로 버려도 된다고 보았다는 것이다.

헤겔은 뉴턴이 이런 식으로 사라지는 크기로 되돌아간 것은 수학적 증명 과정에서 dx와 dy가 비례 관계로 묶이지 않고 각자 독립적으로 출현하므로, 이를 최종 비례의 계기로 보지 않고, 사라지는 크기로 파악하게 되었다고 한다.

헤겔은 미분 계산에서 dx, dy는 단적으로 dy/dx의 계기로서만 여겨져야 하는데도 “특히 그런 기호를 적용하는 데서 기계적으로 계산하는 가운데 미분 계수의 양 측면[dx, dy]이 서로 떼어 내진다는 것으로부터 그런 계산이 끌어내는 장점이 사라진다”(논리학 재판, GW21, S. 265)고 한다. 여기서 그 계산이 지닌 장점이란 곧 미분을 비례로 이해함으로써, 미분 계산이 부딪힌 모순이 해결되는 장점을 말할 것이다.

이상과 같이 헤겔은 뉴턴의 미분을 이론에서는 최종 비로 파악했음에도 불구하고 적용에서는 이를 다시 사라지는 크기로 이해하는 잘못을 서술한 다음, 최종 비의 개념이 비례의 한계라는 개념으로 전개될 수 있다고 말한다.

비례의 한계란 곧 dy/dx가 질적인 크기로서, 일정한 한계를 지닌다는 것을 말한다. 물론, 이 한계는 곧 가변적 크기의 함수 즉 원래 함수 관계에 있는 x, y 즉 F(x)가 지닌 한계다. 질적 한계(dy/dx)를 이루는 두 요소 dx, dy는 오직 이런 관계 속에서 계기로서만 존재하며 더는 독자적인 정량으로서 존재하지 않는다.

이미 말했듯이 정량에서는 한계가 자기에 외면적이다. 그러므로 항상 자기 스스로 증가하거나 감소할 수 있다. 이런 정량은 그 한계 즉 규정이 자기에 외면적이니, 서로 동일하면서도 서로 무차별하다. 여기서 독특한 양적 관계 즉 연속성과 불연속성의 이중성이 출현한다.

그러나 비례에 이르면, 한계는 다시 내면화하면서 고정된다. 하나의 질적인 한계 즉 어떤 규정은 내면화되는 동시에 다른 질적 한계나 규정과 대립 관계 속에 놓여 있다. 이제 하나의 비례 규정은 타자와 대립해서 자기를 규정한다.

이런 비례의 한계 개념에서는 앞에서 말했듯이 dx가 0으로 수렴하더라도, 비례의 한계 즉 dy/dx는 0/0이 아니라 일정한 값을 지니게 된다. dx 즉 증분은 끊임없이 0에 다가가는 점근적인 것이더라도, 비례의 한계는 일정하다. 그러므로 이런 비례의 한계 개념은 사라지는 크기로서 증분 또는 미분이라는 개념에서 해방된다.

“미분 계산에서 dx, dy로 출현하는 무한소는 어떤 유한적이지 않은, 주어지지 않는 크기가 지닌 부정적 공허한 의미를 더는 갖지 않을 뿐만 아니라 양적인 것의 질적 규정 즉 비례의 계기 그 자체라는 특정한 의미를 지닌다.” ”(논리학 재판, GW21, S. 265)

사라지는 크기라는 개념은 여전히 정량의 개념에 머무른다. 그러나 최종 비, 또는 비례의 한계라는 개념을 통해 진정한 무한의 개념이 출현하며, 정량은 그 자체로서 지양되면서 질적인 크기 즉 비례의 계기가 된다. 헤겔은 이를 “유한한 크기가 무한한 크기로 전환한다”라고 말한다.

“지적된 바와 같이 소위 미분은 비례의 양 측면 즉 정량이 사라짐을 표현하며[사라지는 크기] 남아 있는 것은 양적 비례이어서 그런 한 순수하게 질적인 방식으로 규정된다. 질적 관계는 여기서 사라지지 않으니, 오히려 바로 유한한 크기가 무한한 크기로 전환하는 결과로 나오는 것이다.” ”(논리학 재판, GW21, S. 268)

유한한 크기 즉 정량과 무한한 크기 즉 비례는 서로 다르다. 구체적 예를 들어 원호는 정량으로 본다면, 할선보다 클 수밖에 없다. 할선은 직선이며 두 점 사이에 최단 거리기 때문이다. 그러나 원호를 무한한 할선으로 구분하면, 무한한 원호는 무한한 할선과 같게 된다.

또 운동을 예로 들어 볼 때, 곡선 운동과 직선 운동의 관계도 마찬가지다. 양적으로 양자는 다르지만, 무한한 크기로서는 양자는 같다. 즉 가속 운동[ungleichfoermige Bewegung]에서 무한히 작은 시간에 지나가는 거리는 등속 운동[gleichfoermige Bewefung]에서 무한히 작은 시간에 지나가는 거리와 같다.

주석1을 마치면서 헤겔은 마지막으로 수학적 방법의 한계를 지적한다. 그는 옛날의 해석학자는 해석학을 어디까지나 구체적 대상과 관계하여 전개했다. 이때 구체적 대상이란 바로 공간적 관계나 역학적 운동을 말한다. 사실 뉴턴은 경험적으로 증명된 것 즉 갈릴레오에 의해 발견된 낙하 법칙이나 케플러에 의해 발견된 천체 운동 법칙을 그의 미적분론을 통해 정당화했을 뿐이다.

그러나 헤겔 당시 해석학자는 구체적 대상과 관계 속에서 지닌 실질적 의미를 무시하고 전적으로 추상적인 수학적 방식으로 발전시키는 동시에 이를 모든 대상에 무차별적으로 적용하려 했다고 비판한다. 이들은 수학의 지위를 경험을 넘어 고양하면서 수학적 사유에서 자연법칙을 끌어내려 했다.

“그런 명제는 역학의 근대 해석학적 형태에서는 전적으로 계산의 성과로서 소개되며 그런 명제가 실질적인 의미를 지니는 것인지 즉 어떤 실존이 그런 명제 자체에서 독자적으로 어떤 상응하는 의미를 지니는지를 전혀 고려하지 않으며 또한 그런 것의 증명도 고려하지 않는다.””(논리학 재판, GW21, S. 271)

“단순한 계산을 통해 경험을 넘어서 제시되는 법칙, 어떤 실존도 갖지 않은 실존 명제를 발견하려는 시도가 학문의 승리로 과장되고 있다.””(논리학 재판, GW21, S. 271)

“그와 같은 가상을 사람들은 단순한 믿음이나 경험적 지식보다 항상 더 우선시했다. 그러나 나는 이런 방식이 단순한 주머니 돌리기 요술이나 증명하는 체하는 것 이상의 것이 아니라고 여기며 그 아래에 뉴턴의 증명조차 집어넣는데 굳이 숙고해볼 필요조차 느끼지 못한다.””(논리학 재판, GW21, S. 272)

그러나 헤겔은 이런 수학의 월권을 비판한다. 수학은 경험을 통해 이미 발견된 법칙을 정당화하는 도구에 지나지 않는다는 것이다. 또한, 미적분론은 자기 제곱이 가능한 대상 즉 공간이나 역학적 운동에서나 타당할 뿐이라고 한다.

5) 이상 헤겔이 수학적 무한성이라는 이름으로 주석 1에서 전개한 내용을 간단하게 정리해 보았다. 주석 2와 주석 3은 재판에서 추가한 것이다. 주석 2는 방정식의 본질에 대한 설명을 제외하고는 주석 1의 내용과 거의 합치한다. 주석 3은 적분 개념을 통해 다시 수학적 무산성을 소개하는데, 주요 내용은 미적분은 수적으로는 거듭제곱의 함수에서 적용되며 구체적으로는 공간 운동이나 역학적 운동에 적용될 수 있을 뿐, 모든 운동에 적용할 수는 없다고 한다. 이미 주석 1에서 충분히 설명한 부분이라 더 구체적인 소개는 생략하려 한다.

헤겔 형이상학 산책54-미적분은 정당한가(3)[흐린 창가에서-이병창의 문화비평]

2025년 12월 20일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책54-미적분은 정당한가(3)

앞에서 헤겔은 자신의 진정한 무한성 개념을 소개했다. 이를 간단하게 요약하자면 다음과 같다. 그것은 곧 두 정량 사이의 관계 또는 비례다. 여기서 각 계기는 다른 계기에 관계하여 규정되는 것이므로, 이런 관계는 질적인 것으로 된다.

이 질적 크기는 수적으로는 분수로 표현된다. 이런 무한량 가운데 거듭 제곱의 관계에 있는 것이 곧 분수 가운데 정수비로 환원되지 않는 루트나 파이로 표현되는 분수다. 수적인 제곱 관계는 구체적으로는 길이나 면적, 부피의 관계나 물체의 공간적 운동을 표현한다. 바로 이런 거듭제곱의 관계에서 성립하는 것이 미적분이다.

헤겔은 이처럼 미적분이 적용되는 무한량, 그 가운데서도 거듭제곱의 관계를 소개한 다음, 드디어 미적분을 구체적으로 분석하기 시작한다. 그는 이때 특히 뉴턴의 방식에 주목했는데, 그 이유는 뉴턴에 이미 진정한 무한성 개념이 비록 뉴턴 자신은 알지 못했더라도 출현했다는 것이다. 헤겔은 “그 규정의 발견자(즉 뉴턴이다)는 그 사상을 개념으로 아직 정초하지 않았기에 그것을 적용할 때에는 그와 같은 더 나은 상태에 모순되는 방편이 필요했다”(논리학 재판, GW 21, S. 253)라고 말한다. 그렇다면, 뉴턴이 발견하지만, 자각하지 못한 것은 무엇인가?

뉴턴은 미적분을 유출법이라고 했다. 이 유출법의 방식은 그 이전(페르마와 데카르트 그리고 뉴턴의 스승 배로우에 이르기까지)의 무한소 개념에서 기초하는 것이다. 다만 그들이 무한소 또는 “불가분적인 것이라고 이해한” 무한 개념을 뉴턴은 다르게 이해한 것이다. 즉 “사라지는 가분적인 것”(논리학 재판, GW 21, S. 253)으로 이해한다. (여기서 뉴턴은 이 사라지는 것이 단순히 정량이 아니라 정량의 관계 즉 비례라는 점을 강조하는데, 그 점은 나중에 보도록 하자)

우선 미분법을 이해하기 쉽게 다음과 같은 도해를 보기로 하자. 아래의 도해에서 보듯이 곡선 F(x) 상에서 점 p1, p2가 있다고 할 때 두 점을 이으면서 곡선을 자르는 할선의 기울기는 이를 통해 이루어지는 작은 삼각형의 세로/가로 곧 F(x+h)-F(x)/ h이다. 이 식을 풀어서 두 번째 항 이하를 버리면, 미분식이 발견된다.

예를 들어 F(x)가 이차함수 x²이라면, 이 할선의 기울기는 (x+h)²-x²/h이며 이 식을 이항 정리를 통해 풀어보면 2x*h/h+h/h*h가 된다. 이 식 가운데 h/h는 1이니 남는 것은 2x+h이다. 미분의 계산법에서는 이 h는 0으로 간주하고 버리며, 그 결과 미분은 곧 2x로 규정된다.

문제는 h/h가 1이라는 것과 남는 h가 0이라면서 버리는 이유 또는 정당성에 관한 것이다 페르마에서 데카르트에 이르기까지 h는 무한소이며 크기가 없는 것 즉 0으로 간주한다. 따라서 h를 버리는 것은 문제가 없는데, 문제는 h/h다. 이것은 0/0이 되면서 악마의 소굴에 빠져 버리고 만다. 이것이 바로 앞에서 무한소 개념이 가지는 모순이라고 했다.

이 모순을 벗어나기 위해 라이프니츠는 이 무한소를 최소값으로서 0이 아니라, 무한히 작아질 수 있는 크기로 보았다. 그것은 0은 아니고 0에 다가가는 수로 규정되는데, 이것이 바로 앞에서 칸트가 설명한 무한진행이라는 개념이다.

라이프니츠의 무한진행으로서 무한소를 헤겔은 ‘사라지는 크기’ 즉 ‘무한히 가분적인 것’로 규정한다. 이 말 자체는 뉴턴이 쓴 말과 같지만, 라이프니츠에서 사라지는 것은 곧 정량, 크기다. 그러면 h/h가 1이라는 것은 이해된다. 하지만, 이번에는 나머지 h를 버리는 것이 문제다. 라이프니츠는 이 사라지는 크기를 아주 사소한 크기니, 버려도 무방하다고 보았다.

울프는 라이프니츠를 옹호하면서 실제 측정술에서 산의 높이를 잴 때 순간적으로 부는 바람 때문에 모래가 날아가 사라진 것은 계산에 빼도 무방한 것처럼 또는 일식이나 월식을 잴 때 집이나 탑의 높이를 무시하는 것처럼 미분 계산법에서도 아주 작은 크기는 버릴 수 있다고 했다. 그러나 이 h는 무한히 사라지기는 하지만, 그래도 일정한 크기를 가진 것이니, 수학적 엄밀성을 위해서는 버릴 수 없다.

이런 문제점을 해소하기 위해 뉴턴은 ‘최종 비’라는 개념을 제시했다. (뉴턴은 이를 사라지는 크기라고도 했는데 여기서 크기는 곧 비례를 의미한다.) 즉 h가 아무리 작아지더라도 h/h는 일정한 크기의 한계를 지닌다는 것이다. 아래 도해를 보면, 할선의 기울기가 점차 접선에 다가가는 것을 볼 수 있다. 최종적으로 h=o가 되더라도 h/h는 일정한 비율(즉 접선의 기울기)로 남는다. 이것이 바로 최종 비이다.

헤겔은 이처럼 일정한 크기가 유지될 때 그 비례를 뉴턴이 최종 비라고 할 때 마음에 품었던 것이라고 본다. 이런 최종 비에서는 분자와 분모를 이루는 두 정량은 독자적인 정량이 아니다. 두 정량은 하나의 관계 속에서 통일되어 있으니, 여기서 두 정량은 비례의 계기에 불과하며, 서로가 아무리 줄어들더라도 일정한 비례를 유지하면서 줄어드는 것이다. 다시 말하자면, 하나의 계기는 다른 계기를 통해서만 규정되는 것이다.

그런 점에서 헤겔은 뉴턴이 자기가 말하는 진정한 무한성으로서 비례 개념에 도달했다고 본다. 만일 그렇게 된다면, h/h는 1로 받아들이고 반면 h는 버리는 이유가 정당화된다. 전자는 최종 비이며 h가 아무리 줄어들더라도 비례를 유지하지만, 후자 h는 줄어들면 마침내 0이 되면서 사라지는 것이다.

h가 사라지면서 오히려 미분 계산의 정확성이 상실되는 것이 아니라 그 정확성이 오히려 회복된다는 사실은 기하학적으로 증명될 수 있다. 아래와 같은 도해를 보자.

이 도해에서 보듯이 h가 줄어 들면(h->h’->h’->0′) 할선이 점차 점p에서의 접선에 가까워진다는 것을 알 수 있다. 바로 이 접선이 바로 구하려던 곡선의 기울기 즉 미분이다. 이처럼 기하학적으로 보면, 미분은 기울기가 지니는 한계 즉 극한을 의미하게 된다.

“그러나 비례 아래서 사라지는 크기는 사라지기 전에서도 아니고 사라진 이후에서도 아니며 오히려 그와 더불어 사라지는 가운데 있는 비례로 이해되어야 한다. 마찬가지로 생성하는 크기의 최초 비례는 그것이 생성하는 비례다.”(논리학 재판, GW 21, S. 253)

“이런 오해를 피하기 위해 그는 최종 비는 최후의 크기가 지닌 비례가 아니라 한계 없이 줄어드는 크기의 비례가 주어진 모든 유한한 차이보다 더 가까이 다가가는 한계다. 그런 한계를 최종 비는 무가 될 만큼 넘어서지는 못한다.”(논리학 재판, GW 21, S. 254)

현대에서 수리철학자 코헨과 바이어스트라세는 미분을 정의하면서 이런 극한 개념을 사용한다. 이 극한 개념은 헤겔이 뉴턴으로부터 발굴한 최종적 비례, 또는 비례의 한계를 의미하며 그런 한 코헨과 바이어스트라세는 헤겔의 개념 분석의 도움을 받았다고 하겠다.

“한계라는 표상에는 사실 가변적 크기의 질적 비례 규정이라는, 앞에서 제시된 진정한 범주가 들어 있다. 왜냐하면, 그런 가변적 크기로부터 등장하는 형식 즉 dx, dy는 단적으로 dy/dx의 계기로서만 여겨져야 하며, dy/dx 라는 기호 자체는 불가분적인 유일한 기호로 여겨져야 하기 때문이다.”(논리학 재판, GW 21, S. 265)

뉴턴은 이 최종비라는 개념을 이제 ‘생성하는 크기[genita]’, ‘생성의 원리’로 이해한다. 그것은 순간적인 증분이나 감분인데 곧 이 생성하는 크기는 무한소나 무한진행으로 여겨져서는 안 된다. 왜냐하면, 여기서 증분이나 감분은 어디까지나 비례 관계 속에 있는 하나의 계기이기 때문이다.

이런 순간적 증분이나 감분에 의해 이루어진 결과 변화된 운동은 하나의 독자적 정량이며, 뉴턴은 이를 생성의 원리로부터 생성된 크기로 간주한다. 양자는 생성에서 저차적인 질서와 고차적 질서로 구분된다.

이런 설명은 뉴턴이 미분을 이처럼 운동, 생성의 개념으로 이해한 것을 잘 보여준다. 미분은 어떤 것이 운동할 때 어떤 순간에 운동을 변화시키는 힘을 말한다. 생성된 크기가 어떤 정량이라면, 생성하는 크기는 질적인 것이다. 전자는 현존의 무차별성, 외면성 속으로 이행한 것이며 후자는 타자와 관계 속에 규정되는 계기다. 그러므로 헤겔은 전자와 후자가 수적으로 표현되는 방식이 다르다 한다. 전자가 x, y로 규정된다면 후자는 dx, dy로 규정된다.

‘사라지는 크기[Letzte Groesse]’ 즉 정량의 무한진행이나 ‘최종 비[Letzte Verhaltnisse]’ 즉 비례의 무한진행은 유사한 듯 보이는데도 마땅히 구별돼야 한다. 정량은 무한히 사라지더라도 일정한 크기를 유지한다. 그것은 결코 0이 될 수 없다.

그러나 비례의 무한진행은 비례 자체에서 분자와 분모를 이루는 크기는 비례 관계에 묶여 있어 아무리 줄어들더라도 일정한 비례 관계를 유지하지만, 비례를 벗어나게 되면 각 정량은 독자적으로 줄어들면서 마침내 0에 이르게 된다. 아래 두 인용문을 비교해 보라.

-사라지는 크기

“이런 표상이 사태의 진정한 본성을 표현하는 조건은 정량이 무한진행 속에서 갖는 정량의 항상성이 정량이 사라지는 가운데 자기를 연속하면서, 자신의 피안에 다시 다만 어떤 유한한 정량을 즉 급수[계열]의 새로운 항이 발생하게 되는 것이다.”(논리학 재판, GW 21, S. 254)

-사라지는 비례

“그러나 진정한 무한 속에서 만들어지는 이행에서는 항상적인 것은 비례다. 그 비례는 아주 항상적이고 자기를 보존하기에 그런 이행은 오히려 다만 그 비례를 순수하게 드러내는 데 성립하며 또한 비례의 두 측면을 이루는 정량이 이 비례 밖에 놓이면서도 여전히 정량이 되게 한다는 사실 즉 관계없이 존재한다는 규정이 사라지게 한다는 것이다.”(논리학 재판, GW 21, S. 254-255)

헤겔은 이와 연관하여 오일러의 주장을 소개한다. 오일러는 뉴턴의 최종비 개념을 근거로 하여 h/h는 1이지만, h=0이라는 주장을 이렇게 설명한다.

“무한한 차이[미분]은 다만 정량의 0이지, 질적인 0은 아니며, 정량의 0이더라도 단지 비례의 순수 계기이다.”(논리학 재판, GW 21, S. 257)

오일러는 0/0의 모순을 피하기 위해 산술적 비례와 기하학적 비례를 구분했다. 수학적 비례에서 0/0은 악마의 소굴이 되더라도 기하학적 비례에서는 0/0은 일정한 값을 지닐 수 있다고 한다. 헤겔은 오일러가 기하학적 비례라고 한 것은 다름 아닌 뉴턴이 최종비라고 말한 것에 해당한다고 본다.

헤겔 형이상학 산책53-미적분은 정당한가(2) [흐린 창가에서-이병창의 문화비평]

2025년 12월 16일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책53-미적분은 정당한가(2)

앞의 글에서 헤겔은 미적분을 정당화하는 개념으로 무한소나 무한진행을 비판하면서, 자신의 무한 개념 즉 진정한 무한을 설명했다. 진정한 무한은 두 정량 사이의 비례 관계이며, 타자를 통해 자기를 규정하는 것이며 질적인 크기라고 했다.

이런 무한량의 개념은 이미 양적 무한성을 다룰 때 헤겔이 설명한 것인데, 아직 이 무한량이 미적분을 어떻게 정당화하는지는 설명되지 않았다. 그런 설명은 주석 1의 후반부에 들어가서 구체적으로 소개되는데, 이에 앞서서 헤겔은 이런 진정한 무한성의 개념을 수적으로 표현하는 문제에 다시 골몰한다.

무한량은 수적으로는 분수로 표현된다. 헤겔에서 셈은 곧 새로운 수를 낳는데, 더하기 빼기는 정수에 머무른다. 곱하기에 이르면 이미 두 개 정량의 관계가 출현한다. 곱하기는 더하기로 환원될 수 있다. 3*4는 세 번씩 더하기를 네 차례 걸쳐 계속하면 얻어진다. 그러나 곱하기의 진정한 의미는 두 정량의 관계에서 드러난다. 3미터 길이를 폭으로 4미터 이동한 것일 수 있으며, 시간 당 3키로 속도로 네 시간째 달린 거리일 수도 있다.

그러나 곱하기는 흔히 더하기로 환원되면서 두 정량의 관계는 감추어지고 마는데, 이 두 정량의 관계는 곱하기를 뒤집은 셈인 나누기에서 분명하게 드러난다. 나누기는 두 개의 정량이 서로 관계한다는 것을 분명하게 표현한다. 예를 들어 2/7이 그렇다. 두 개 정량의 차이와 동시에 관계가 빗금[/]을 통해 분명하게 드러난다.

나누기를 표현하는 분수는 두 개 정량의 관계라는 점에서 이미 무한량을 표현한다. 그러나 정수비로 환원될 수 있는 분수는 무한량을 은폐한다. 그것은 독자적인 하나의 정량을 표현하는 것으로 여겨진다. 그러나 정수비로 환원될 수 없는 분수가 있다. 그것은 예를 들어 무리수나 통약불가능한 수(예를 들어 원주율)를 표현하기도 한다. 이런 표현에 이르면 이런 분수가 무한량을 표현한다는 것이 더욱 분명하게 드러난다.

헤겔은 무한량을 표현하는 두 개의 표현 형식을 비교한다. 이 두 표현 형식은 정수비가 되는 분수에서도 성립하지만, 여기서는 그 차이가 드러나지 않는다. 반면 정수비가 아닌 분수에서 그 차이는 분명하게 드러난다. 그러므로 후자의 측면에서 두 표현 형식의 차이를 살펴보자. 하나는 무한 계열[Reihe: 급수]의 형식이고 다른 하나는 분수 표현이다.

①: 2/7, 루트 2, 파이

②: 0.285714.., 1.141…, 3.14…

②의 표현 형식을 보면, 무한 계열의 형식으로 표현되어 있다. 이런 표현은 ①을 개수[Anzahl]로 표현한 것인데, 이 경우는 정수비와 달리 결코 최종 결과에 도달하지 못한다. 여기서 표현된 것은 진정한 전체에 비해 모자라며 항을 추가해서 필요한 만큼 더 정확하게 규정할 수는 있지만, 아무리 항을 추가하더라도 모자라기는 마찬가지다. 그러므로 이 규정은 당위에 불과하며 악-무한 또는 무한 진행을 표현한다.

헤겔은 이런 표현은 “질적인 규정성에 기초하는 것을 개수로 표현하려는 것”(논리학 재판, GW21, S. 244)이기 때문에 그런 모순은 해소되지 않는 모순이라고 한다. 또는 표현하는 것은 정량이고 표현되는 것은 무한이니, 양사의 상이성 때문에 도달할 수 없는 피안이라고 말한다. 여기서 도달해야 하는 한계는 자기의 항 밖에 있다.

반면 ①의 표현 형식을 보면 이런 무한 계열로 표현되는 것이 일정한 합에 이미 도달했다는 것을 의미한다. 그 합이 곧 분수며 루트며 파이다. 이런 표현 형식에서는 ②의 표현에서 드러났던 무한성이 다시 감추어진다. 그러나 ①의 표현 형식은 이 무한성이 사실은 두 개의 정량의 관계라는 점이 그것도 일정한 비례 지수 즉 질적인 크기를 가지고 있음을 표현한다. 이런 표현은 무한량의 한계를 직접 표현한다.

“급수는 정립된 항 때문에 무한한 것이 아니라 불완전하기 때문에 즉 그 항에 본질적으로 속하는 타자가 그 급수의 피안에 있기 때문에 무한하다.”(논리학 재판, GW21, S. 245)

“그러나 그 급수에 반해서 유한한 표현 또는 그런 급수의 합이라고 말해지는 것은 결함이 없다. 그런 표현은 급수가 다만 추구하는 값을 완전하게 포함한다. 피안은 도주하는 것으로부터 소환되어서 그런 표현의 본질과 본질이어야 하는 것은 서로 분리되지 않으며 동이한 것이다.”(논리학 재판, GW21, S. 245)

헤겔은 여기서 스피노자의 무한 개념을 소환한다. 흔히 유한은 긍정이고 그 부정인 무한은 부정으로 규정되지만, 스피노자는 유한을 오히려 타자의 부정으로, 무한을 자기 긍정으로 규정한다. 그런 점에서 헤겔은 스피노자의 무한 개념이 진정한 무한성 개념을 함축하고 있다고 본다.

스피노자는 이런 절대적 긍정성으로서 무한 개념을 예를 들어 두 개의 원을 통해 설명했다. 즉 서로 부등한 원이며 하나의 원이 다른 원 안에 있으면서도 서로 중심이 다르면서 서로 접촉하지 않을 때 두 개 원 사이의 공간은 일정한 크기를 지닌 것이지만, 그것을 수를 통해 표현하려 하자면 무한한 계열이 필요하니, 바로 이것이 현존하는 무한성을 잘 보여준다는 것이다.

스피노자는 무한에 관한 무한을 급수나 집합으로 표상하는 것을 내버리고 무한히 현재적이고[gegenwaertig] 완전하다는[in sich vollendet] 사실을 위의 예를 들어 설명했다. 스피노자는 전자를 상상의 무한으로 후자를 사유의 무한으로 부른다. 이 후자가 진정한 무한성[wirkliche Unendlichkeit]이다.

그러나 스피노자에서 자기 긍정으로서 무한성은 절대적 통일, 부동의 통일이며, 그런 점에서 타자를 매개로 해서 자기 내로 복귀한 자기 긍정을 표현하지 못하는 한계를 지닌다고 한다.

이상 헤겔은 진정한 무한성의 개념을 소개했다. 그 무한량은 두 개 정량의 관계로 이루어진다. 이는 수적으로는 분수로 표현된다. 이 분수적 표현을 곱하기의 표현 즉 함수를 통해서도 이해할 수 있다.

수적으로 같은 분수로 표현되더라도, 정수비로서 분수와 무리수와 같은 분수는 구분된다. 정수비는 곱하기로는 y=ax와 같은 함수로 표현된다. 여기서 정수비 a는 고정된 정량 즉 개수를 의미한다. 여기서 서로 함수 관계에 있는 두 정량은 “각자 고립적으로 독자적인 정량이며, 그 함수 관계는 그 수[정량]에 본질적이 아니다.” 즉 그 함수 관계는 두 정량에 대해 무차별하다.

물론 이 사이에도 관계가 있으며 그 관계는 곧 무한량이다. 그러나 그런 무한량은 무한성의 의미를 충분히 드러내지 못한다. 왜냐하면, 이처럼 관계 즉 비례가 그 정량에 외면적이기 때문이다.

이런 정수비에서 무한량은 운동에서는 등속운동과 같은 것이거나 비중(=무게/ 부피)인데, 여기서 미분은 제로라는 점을 생각하면 헤겔이 왜 무한량이 충분히 자기를 드러내지 못한다고 말하는가가 이해된다.

반면, 등가속 운동 즉 Y=1/2at² 이나 포물선 운동 y²=x 는 이와 다른 의미를 지닌다. 여기서 함수의 양 측면은 특정한 정량이 아닐 뿐만 아니라 그 함수 자체가 고정된 정량이 아니라 가변적 크기다. 양자는 제곱 비례하며, 이런 제곱 비례는 비례를 이루는 두 정량과 외면적인 관계에 머무르는 것이 아니라 내적인 관계를 지닌다.

그러므로 여기서 관계하는 정량은 더는 독자적 정량으로 존재하지 않으며, 다만 다른 정량과 관계 속에서만 의미를 지니고 따라서 타자에 대한 관계를 자기에 내재하는 것으로 함축하고 있다.

헤겔이 미적분을 정당화할 때 결정적 의미를 지니는 것이 바로 정수비와 달리 제곱 비례는 관계하는 정량에 대해 내적인 관계라는 것이다. 그러므로 여기서 함수 관계에 있는 x와 y는 독특한 방식으로 표현된다. 즉 dy와 dx인데 이 표현은 사실 라이프니츠가 무한소, 미분을 표현하기 위해 고안한 것이지만, 헤겔은 이를 y/x에서처럼 외면적 관계가 아니라 내적인 관계를 표현하는 것으로 파악한다. 즉 “dy, dx는 더는 정량이 아니며 단지 비례 속에서만 의미를 지닌다”(논리학 재판, GW21, S. 251)는 것이다.

무한량은 두 정량의 관계라 했다. 이 두 정량은 동일한 정량에서 서로 다른 정량일 수도 있고, 종류가 다른 정량일 수도 있다.

처음은 곱해진 것[또는 비례 관계에 있는 것]이 동일한 정량일 때다. 이때 두 정량의 사이는 무차별하며, 외면적이니, 이런 동일한 정량의 관계는 정수비로 표현될 수밖에 없다. 이런 정수비에서도 미적분이 성립하지만, 실상 여기서는 그 의미는 없다. 왜냐하면, 이 경우 미분은 0에 해당하기 때문이다.

또한, 두 정량이 다른 종류일 때 그 관계는 물질적 결합을 의미할 것이다. 예를 들어 원소의 상호침투적인 화학적인 결합이 이에 속한다. 이런 화학적 결합에서는 하나의 정량이 자기를 지양해서 완전히 다른 정량으로 이행하니, 이는 구조적으로는 미분적 관계이지만(상호 침투가 그런 미적분의 관계를 보여준다), 더 이상 수적인 방식으로 표현될 수는 없다. 이것은 수학적 운동을 넘어선 물질의 구체적 운동에 속한다.

수학적인 미적분이 다루어지는 영역은 이 가운데 특히 동일 정량이 거듭제곱의 관계에 있는 경우다. 양자 사이에 존재하는 것이 곧 거듭제곱 도는 자기 제곱이다. 이제 곱하기가 자기 제곱으로 발전하게 되면, 그 결과 새로운 정량이 출현할 때 이런 곱하기는 자기 자신을 제곱하는 것이니, 자기에 내면적인 것이며 이때 곱해진 것들 사이의 관계는 단순한 비례가 아닌 제곱근의 관계에 있다. 이때 비례는 정수화할 수 없는 무한급수의 형태로 출현한다.

자기를 제곱한다는 것은 구체적으로는 길이를 길이로 곱해 면적으로 구하거나 면적을 면적에 곱해 부피를 구하는 것과 같은 운동이다. 물질의 운동 가운데 속도와 가속도, 운동 에너지 사이의 관계도 이런 거듭제곱에 속한다.(여기서 시간은 공간적 길이의 하나로 여겨진다)

“무한은 이런저런 정량으로서 지양될 뿐만 아니라 양 일반으로서 지양된다. 그러나 양적 규정성은 남는다. 그것은 정량의 지반, 원리다. 또는 이렇게도 말할 수 있는데 최초의 개념에 도달한 양적 규정성이다.”(논리학 재판, GW21, S. 251)

미분이 이처럼 공간운동이나 역학적 운동에 한정된다는 사실은 헤겔이 철학의 방법론으로 수학적 방법을 사용하는 것을 기피하는 까닭이 된다. 하지만, 헤겔이 수학적 방법이 양을 다루는 역학의 영역에서 의미가 없다고 보는 것은 아니며, 오히려 양적인 것의 영역에서 가장 적절한 방법은 곧 이런 수학적 방법 즉 미적분이라 본다.

헤겔 형이상학 산책52-미적분은 정당한가?(1) [흐린 창가에서-이병창의 문화비평]

2025년 12월 16일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책52- 미적분은 정당한가?(1)

헤겔은 양적 무한성을 다룬 끝에 주석을 세 개 붙였는데 그 가운데 주석 1은 초판에서 이미 나오지만(내용을 약간 수정했으나 그 수정은 언어적 표현에 그친다), 주석 2와 3은 재판에서 추가한 부분이다. 이 세 주석에서 헤겔이 다룬 것은 소위 미적분의 정당화 문제다.

먼저 주석 1 앞부분에서 헤겔은 자신이 왜 미적분의 정당화에 뛰어들었는가를 설명하는데, 이 부분을 읽어보면, 그의 의도와 그의 목표가 잘 드러나리라 생각한다. 이 부분은 수학을 전공하지 않은 필자로서는 지극히 난해하다. 더구나 헤겔이 수학의 공식을 철학적 개념으로 서술하기에 그의 말이 무엇을 지칭하는지 알기도 힘들다. 그 때문인지, 이 부분에 대한 학계의 논의는 거의 없다. 그런 까닭에 필자는 부득이 헤겔이 주석에서 자기의 논지를 전개한 대로 따라가면서 그의 주장을 요약하려 한다.

주석 1을 시작하면서 헤겔은 이렇게 말한다. 미적분의 정당성은 주로 ‘성과’의 ‘올바름’에 기인하지만, 그 증명은 정당화되지 못했으며, 심지어는 “그 자체로 잘못으로 인정된다”라고 말한다. 이처럼 미적분이 자신이 사용하는 도구의 본성을 알지 못하고 비판 없이 사용된다면 “그 적용의 범위를 결정하지 못하거나 그 오용을 막을 수 없는”(논리학 재판, GW21, S. 236-237) 것이 아닐까?

헤겔은 이런 미적분의 정당화를 수학자의 손에 맡겨두지 않고 자기가 직접 다루게 된 이유로 이 미적분의 토대가 되는 개념이 철학에서 다루는 무한 개념과 관련된다는 사실을 들고 있다. 그는 심지어 “수학적 무한[미적분]에 근저에는 진정한 무한 개념이 놓여 있으며” 이것은 기존의 철학에서 논의된 형이상학적 무한 개념(즉 헤겔의 말로 악무한이나 무한 진행)보다 더 차원 높은 것이라고 말한다.

그런데도 수학은 자신의 근저에 있는 무한성 개념을 드러내지 못하고, 자신을 정당화하지도 못한 채, 그런 철학적 정당화는 자기들이 할 바는 아니며, 자기들은 그저 자기가 처한 고유한 지반 위에서 일관적으로 앞으로 나가기만 하면 된다고 믿으니, 그 때문에 자기가 개입하게 되었다는 말이다.

헤겔은 미적분이 증명 과정에서 오류를 범한다고 했을 때, 그 오류는 간단히 말해 다음과 같다. 즉 미적분은 “유한한 크기를 한번은 무한소만큼 증가시키고 이 무한히 작은 크기를 부분적으로는 그다음 계산에 보존하지만, 일부분은 무시함으로써” 일어난다고 한다. 이처럼 일부를 무시하는 이유는 “그 일부가 영은 아니지만, 너무나도 눈에 띄지 않을 정도의 정량이어서 무시될 만한 것이기”(논리학 재판, GW21, S. 237)때문이라 한다.

예를 들어 y=x² 의 미분 계산에서 도중에 전개한 항 가운데 미분을 포함하는 첫 번째 항 2x*dx/dx는 남기고 두 번째 항 dx²/dx는 제거하는 것을 말할 것이다. 그런데 아무리 사소하더라도 일상적 삶에서와 달리 수학에서는 무시할 수 없는 것이 아닐까? 수학은 엄밀하고 정확한 학문이며 더구나 “수학적 인식에서는 증명이 본질적이기에” 조금이라도 잘못된 증명은 수학에서는 받아들일 수 없기 때문이다. 헤겔의 이 주장은 나중에 상세하게 설명하겠지만, 미적분에 관한 기초만 이해하더라도 충분히 인정할 만한 주장이다.

헤겔은 미적분의 문제점을 이해하기 위해 일단 이렇게 문제점만 던져놓고는 무한량에 대한 앞에서 설명한 개념으로 다시 돌아간다. 왜냐하면, 미적분에서 주로 사용하는 무한 개념이 무한소 개념이기 때문이다.

이 무한소 개념은 역사적으로 고대에서(알키메데스나 카발리에, 페르마 등) 등장해 라이프니츠 직전까지 계속됐기 때문인데 이 개념은 미적분을 설명하기에 충분하지 못하다고 본다. 헤겔은 이 논의에서 미적분을 이해할 수 있는 개념은 이런 무한소 개념이 아니라 자신의 진정한 무한성 개념에 있다는 것을 보여주려 한다.

우선 그는 무한히 작은 양은 정량이 아니라고 한다. 이 무한소는 최소치라는 의미인데 즉 “그것을 넘어서 더 적은 것이 없는 크기”(논리학 재판, GW21, S. 239)다. 그러나 어떤 것이 정량인 한에서는 항상 증감할 수 있다. 증감할 수 있다는 것은 정량의 본성에 속한다. 따라서 최소치란 즉 더 적어질 수 없는 것은 더는 정량이 아니게 된다. 그런데도 무한소는 하나의 크기로 받아들여지니, 무한소란 개념 자체에 자기모순을 지닌 것에 지나지 않는다고 한다.

“왜냐하면, 정량은 무한한 한에서 지양된 것으로 사용되기를 요구하며 즉 정량은 아니면서도 그것의 양적인 규정이 여전히 남아 있는 것으로서 사유되기를 요구하기 때문이다.”(논리학 재판, GW21, S. 239)

헤겔은 이때 즉 무한자가 일정한 크기를 가지게 된다면, “그런 무한에 대해 더 큰 것과 더 적은 것의 구별이 성립한다”(논리학 재판, GW21, S. 240)라고 하니, 나중에 칸토르가 무한 집합론의 모순으로 설명했던 것을 헤겔은 이미 선취하고 있는 것으로 보인다.

칸토르의 모순은 예를 들어 흔히 자연수의 집합은 정수의 집합보다 작은 것으로 여겨지지만, 자연수와 정수는 둘 다 무한한 원소를 지니고 각 원소는 서로 대응하니, 양자는 일대일 대응 관계에 있고 따라서 크기가 같다고 할 수도 있다는 것이다. 자연수의 무한은 정수의 무한보다 크다고 생각하는 상식은 무한을 일정한 값을 지닌 것으로 생각하는 데서 나온 것임을 알 수 있다.

최소치라는 개념을 비판하면서 칸트는 무한량이 되기 위해서는 최소라는 일정한 값이 있어서는 안 되며 이 무한량-칸트는 무한한 전체라는 말로 대체한다.-은 끊임없이 증가하거나 감소하는 운동 중인 것 즉 무한 진행으로서 이해해야 한다고 주장했다. 즉 여기서는 앞에서 주어진 것을 넘어가는 관계만이 들어 있고 주어진 것에 따라서 그것을 넘어선 무한한 전체는 다른 무한한 전체보다 더 클 수도 있고 더 적을 수도 있게 된다. 무한한 전체의 절대적 크기라는 것은 없다는 것이다.

칸트에서 무한량에서 이처럼 주어진 양을 넘어가는 운동은 주관의 작용에 속한다. 주관은 끝없이 주어진 양을 넘어가는 가운데 전체를 동시에 파악하는 “종합은 결코 완성될 수 없게”(논리학 재판, GW21, S. 240, 이 구절은 칸트 재인용) 된다.

이를 거꾸로 보면 주관이 넘어가는 작용을 하지 않는다면 대상인 수 자체는 마침내 완성된 최대치라는 일정한 값을 지니게 되니, 여전히 앞에서 모순으로 여겨진 최대치, 최소치라는 개념이 사라지지 않는다. 다만 여기서는 넘어가는 운동은 주관에 속하고 정량이라는 크기는 대상에 속하면서 “모순이 객체와 주관에 나누어 배당될 뿐”(논리학 재판, GW21, S. 240)이다.

헤겔은 이런 무한 진행 역시 모순을 피할 수 없는데, 이 모순은 미적분에서 분명하게 나타난다. 앞에서 든 이차함수의 예에서 항을 전개하면 첫 번째 항은 2x*dx/dx이다. 이때 뒷부분 dx/dx는 결국 1이니, 여기서는 2x만이 남는다. 그러나 만일 dx가 무한소로서 어떤 값을 지니지 않는다면 즉 마침내 0에 도달하고 마는 무한히 작은 양이라면, dx/dx는 곧 0/0이 되면서 판단 불능에 빠지게 된다.

0/0은 1도 되고 100도 되는 무의미한 수다. 이런 판단 불능을 제거하기 위해서는 dx는 최소의 값을 지녀야 하며 그때 비로소 미분 계산에서 첫째 항에서 2x만을 남기는 이유가 이해된다.

헤겔은 마침내 자신의 무한성 개념을 제시한다. 그의 무한성 개념은 이미 앞에서 제시한 대로 비례(또는 관계 Verhaltnisse]의 개념과 연관된다. 그는 앞에서 외연량과 내포량을 설명한 다음, 무한량을 제시했다.

외연량은 단순한 자기 관계다. 이는 추상적이며 개별적인 정량이다. 이 정량이 자기의 임의적인 한 부분을 단위(예를 들어 보폭이나 팔길이)로 측정되면, 일정한 정량이 된다. 예를 들어 길이나, 무게 등이 여기에 속한다. 이 외연량은 ‘배중성[Vielfachheit]’으로 규정된다.

내포량은 여전히 개별적이며 추상적 정량이지만, 타자와 비교된 정량이다. 더 크거나 더 적은 것을 순서대로 하면, 첫 번째, 두 번째, 세 번째 등이다. 예를 들어 경도나 강도가 여기에 속한다. 헤겔은 이런 외연량을 ‘다중성[Mehrheit]’이라고 한다.

무한량은 타자를 통해서 측정된 정량이다. 예를 들자면 속도(=거리/시간)나 비중(=무게/부피)다. 이는 두 개의 정량 사이의 관계가 바탕이 된다. 즉 그 관계를 통해서 어떤 것이 자기를 규정할 때, 그것이 무한량이다. 타자를 통해 자기를 규정한다는 점에서 이 무한량은 부정성을 지니고 따라서 질적인 규정성을 지닌다. 그러나 무한량은 독자적으로 하나의 정량이므로 이는 “질적 형식을 취하고 있는 크기 규정”(논리학 재판, GW21, S. 241)이다.

“무한 정량은 계기로서 그 타자와 본질적으로 통일 속에 있으며 다만 그의 타자에 의해서 규정되는 것으로서만 존재한다. 즉 무한 정량은 그의 타자 존재와 관계 속에 있는 것과 연관해서만 의미 있는 것일 뿐이다.”(논리학 재판, GW21, S. 241)

질적인 것은 일반적인 것이다. 빨간색은 꽃의 빨간색일 수도 있고 석양의 빨간색일 수도 있다. 마찬가지로 무한량이 질적 성격을 지닌다는 것은 그 성격이 일반적이라는 말이 된다. 여기서 일반성은 비례의 일반성이다. 헤겔은 이 무한량을 ‘비례의 지수[Exponent]’라고 말한다.

즉 어떤 정량의 크기가 다른 정량의 일정한 크기를 단위로 해서 측정된 것이므로, 이 관계 즉 비례 관계는 일정하다. 다른 정량의 단위가 증가하면 그것에 비례해서 어떤 정량의 크기도 변화한다. 예를 들어 속도나 시간당 4키로라면 두 시간에는 8키로 거리를 지나가며 세 시간에는 12키로 거리를 지나간다.

무한량에서 서로 관계하는 두 정량은 독자적으로 보면 하나의 정량이지만, 이 관계에 들어가면 더는 정량이 아니라 전체 정량의 한 계기로서만 존재한다. 하나의 정량은 양적인 것으로서 다른 정량에 대해 무차별하겠지만, 전체의 계기로서의 정량은 자신과 관계하는 타자(다른 정량)에 대해 일정한 관계를 유지한다.

이 무한량은 자기 관계하는 것이다. 즉 자기가 자기를 단위로 측정된다. 그러나 이는 외연량처럼 추상적인 자기 관계가 아니라 타자를 매개로 해서 측정된 자기 관계다. 예를 들어 속도는 거리의 크기를 말한다. 크기는 자의적인 척도를 통해 측정된다면, 단순한 자기 관계다. 그러나 이 크기가 다른 정량인 시간에 관계하여 측정된다면 그것이 속도다.

헤겔은 미적분에서 핵심 개념인 무한은 알키메데스의 무한소도 아니며, 칸트의 무한 진행도 아니고 바로 이런 관계로서의 무한량을 의미한다고 본다.

헤겔 형이상학 산책 51-시공간은 무한한 것인가? [흐린 창가에서-이병창의 문화비평]

2025년 12월 5일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책 51-시공간은 무한한 것인가?

시간, 공간은 무한한가? 앞에서도 밤하늘 무한한 천공 앞에서 숭고함을 느끼거나 시냇가 조약돌에서 아득한 시대 화석으로 남은 생물을 발견하면, 그 아득히 먼 시대를 상상하며 즐거움을 느낀다.

시간과 공간의 아득함에 관해 시인들은 많은 시를 지었는데, 헤겔은 양적 무한성을 다루면서 주석에서 할러의 시를 하나 인용한다.

숱한 산들처럼
엄청난 수를 쌓아 올리고
시간의 더미에 시간을, 세계의 더미에 세계를 쌓아 올리고
그리고 소스라칠 정도로 높은 곳에 올라가
아득하게 다시 너를 내려다보면,
수의 위력이 천 배가 증가하더라도,
아직도 너는 단 한 귀퉁이조차 드러나지 않는다.
차라리 내가 수의 위력을 떨쳐버릴 때
너의 모습은 생생하게 내 앞에 떠오를 것이다.

헤겔은 이 시의 앞부분은 무한한 시공간 앞에 느끼는 숭고함을 표현했으나 이 시의 마지막 부분이 오히려 의미심장하다 한다. 즉 차라리 무한한 수의 위력을 떨쳐 버릴 때 오히려 무한의 진정한 모습이 생생하게 떠오른다는 것이다.

헤겔이 말하는 수의 위력이란 곧 무한 진행으로서 악 무한을 의미할 것이다. 반면 진정한 무한의 모습은 곧 내재하는 무한성 즉 자기 부정성으로서 무한성일 것이다.

우리 앞에 있는 세계의 무한성에 관한 논의는 곧바로 세계의 유한성이라는 주장으로부터 반박당한다. 세계에 시초가 있어야 하고 우주는 그 한계가 있어야 한다. 그럴 때만 이 세계가 존재할 수 있는 것이 아닌가? 그러나 이런 주장을 통해서도 무한성에 관한 주장이 완전히 사라지지 않으니, 형이상학의 세계는 곧 세계의 무한성과 유한성이라는 주장의 전장터가 되었다.

이런 전장을 최종적으로 흽쓸어 버리려 했던 철학자가 곧 칸트였으니, 칸트는 순수이성 비판에서 무한성이라는 주장이든 유한성이라는 주장은 이율 배반에 빠지고 만다는 것을 논증했던 것으로 유명하다.

칸트는 알다시피 순수이성 비판 변증론 2편 2장에서 순수이성의 이율 배반을 다루면서 네 가지 이율 배반을 제시했다. 이 네 가지 이율 배반은 네 가지 판단형식의 범주 즉 질적 범주, 양적 범주, 관계적 범주, 양상적 범주에 각기 해당한다.

그 가운데 질적 범주에서 나타나는 이율 배반은 사물이 합성체인지 단순 실체인지 하는 이율 배반인데, 칸트는 이를 두 번째 이율 배반으로 다루었지만, 양적 범주보다 질적 범주를 우선하는 헤겔은 오히려 앞에서 질적 판단형식을 다룰 때 이미 다루었다.

헤겔은 양의 무한성을 논하는 가운데 칸트가 말한 첫 번째 이율 배반을 다룬다. 헤겔은 이 이율 배반이 양적인 것과 관계한다고 보았기 때문이다. 그 때문에 헤겔에서는 이 이율 배반이 두 번째로 나타나는데, 그것은 곧 시간과 공간이 시초나 한계를 지니는 것인가 하는 문제인데, 이는 다시 말하면 세계가 양적으로 유한한가 아니면 무한한가 하는 문제라고 볼 수 있다.

헤겔은 이 문제를 다루면서 시간과 공간에 대한 이해가 자신과 칸트가 다르다는 것을 전제로 한다. 칸트는 시간과 공간을 직관의 형식으로 보았다. 반면 헤겔은 시간과 공간은 사물의 상호 관계하는 방식이라고 규정한다.

이때 관계 방식은 바로 양적인 것의 방식인데, 앞에서도 말했듯이 이 방식은 서로 동일한 일자와 일자의 외면적인 관계다. 나뭇잎과 나뭇잎, 물방울과 물방울의 관계에서 나뭇잎이나 물방울과 같은 구체적 대상을 제거한다면 바로 시간 공간적 관계가 된다. 이런 시간, 공간적 관계는 사물이 가진 모든 관계를 의미하지 않는다. 그것은 사물이 지닌 모든 구체적 관계를 추상한 가장 외면적인 관계일 뿐이다.

칸트와 같이 추상적인 직관의 형식으로 보든, 헤겔과 같이 사물의 가장 외면적인 관계로 보든 일단 양적인 관계 즉 일자와 일자의 관계라는 점에서는 동일한데, 헤겔은 이런 양적인 관계에서 시간과 공간의 유한성과 무한성의 문제를 여기서(정량, c 절 양적 무한성, b 항 무한 진행, 주석 2) 다룬다.

우선 정립은 세계가 유한하다는 주장이다. 구체적으로 시간에는 시초가 있으며 공간에는 한계가 있다는 주장이다. 헤겔은 우선 이 정립에 관한 칸트의 증명을 인용하면서 소개하는데, 다음과 같다.

“세계가 시간상 시초를 갖지 않는다면 주어진 시점에 이르기까지 영원이 흘러가야 하며 세계 속에 상호 뒤따르는 사물 상태의 무한한 계열이 지나가야 한다. 그러나 이제 이런 계열이 무한하다는 것은 곧 이 계열이 계기적 종합을 통해서는 결코 완전해질 수 없다는 것을 의미한다. 그러므로 무한히 흐르는 세계 계열은 불가능하다. 따라서 세계의 시초는 세계가 현존하기 위한 필연적 조건이고 이것은 처음 증명되어야 했던 것이다.”(칸트 재인용, 논리학 재판, GW21, S.229)

칸트의 증명은 간단하다. 시초가 없다면 어떤 현존도 있을 수 없다. 왜냐하면, 현존에 이르기 위해서는 무한한 계열이 지나가야 하는데 이 무한한 계열을 다 지나가는 것은 불가능하기 때문이다. 그러나 이 세계에 어떤 현존이 있는 것을 분명하므로, 시초가 없을 수 없다는 것이다.

헤겔은 이어서 공간의 한계에 관한 칸트의 증명을 소개한다. 이 부분은 칸트의 증명을 헤겔이 요약하는 방식으로 소개된다.

“공간상 무한한 세계 부분들의 총괄을 위해서는 무한한 시간이 요구될 것이다. 세계가 공간 속에서 형성되는 것으로서가 아니라 완전히 주어진 것으로서 여겨지는 한, 무한한 시간은 이미 흘러간 것으로 여겨져야 한다. 그러나 시간에 관한 증명의 앞부분에서 제시됐듯이 무한한 시간이 흘러간 것으로 여겨지는 것은 불가능하다.”(논리학 재판, GW21, S.229)

이 증명의 핵심은 곧 공간이 한계가 없다면, 이 공간을 총괄하기 위해 무한한 시간이 걸리는데, 무한한 시간이 흘러가는 것은 불가능하니, 공간은 한계가 있어야 한다는 것이다. 여기서 공간을 우리가 총괄할 수 있다는 것이 전제된다.

위와 같이 칸트의 정립을 소개한 다음 헤겔은 이를 비판하는데, 그의 비판은 칸트의 소위 귀류법적인 증명은 증명 속에 증명돼야 하는 것이 이미 전제되고 있다는 비판이다. 구체적으로 말해서 이미 칸트는 시간에는 시초가 있고, 공간은 한계가 있어서 총괄 가능해야 한다는 것을 전제로 한다.

이것은 세계에서 현존이 있으려면 요청되는 것인데, 증명을 통해 증명돼야 하는 사실이다. 칸트의 정립 증명은 시간의 시초가 있고 공간의 한계가 있어야 하므로, 무한한 시간과 무한한 공간은 없어야 한다는 주장이니, 사실 동어반복에 지나지 않는다.

그러나 현존이 있기 위해서 반드시 시간의 시초와 공간의 한계가 있어야 하는가? 어떤 것은 그 시초를 모르는 것이거나 공간상 한계 없이 펼쳐지는 것이더라도 현존할 수 없는 것은 아니다. 아무도 내 앞의 우주가 언제 생겼는지, 어디까지 펼쳐지는지 모르더라도, 내 앞에 우주가 있다는 사실은 알고 있다.

“증명되어야 하는 주장이 증명의 근저에 직접 놓여 있으므로 증명을 우회적으로 만들거나 증명을 한다는 것 자체가 불필요한 것을 알 수 있다. 즉 영원(영원은 여기서 다만 악 무한적인 시간이라는 형편없는 의미를 지닌다)이 흘러가야 도달할 수 있는 어떤 시점 또는 각 주어진 시점이 전제된다. 주어진 시점이란 곧 시간 속에 일정한 한계를 의미할 뿐이다. 그러므로 증명에는 시간의 한계가 실제로 있는 것으로 전제된다. 그러나 그런 한계는 증명돼야 할 것이다. 왜냐하면, 정립이 주장하는 것은 곧 세계가 시간상 시초를 갖는다는 것이기 때문이다.”(논리학 재판, GW21, S.229)

이어서 헤겔은 반정립을 살펴본다. 칸트가 말한 반정립은 세계는 시초를 갖지 않으며 공간상 한계도 갖지 않고 오히려 시간상이나 공간상으로 무한하다는 주장이다. 이에 대한 칸트의 증명은 다음과 같다.

“세계가 시초를 갖는다 하자. 현존하는 이 시초에 앞서 사물이 존재하지 않는 시간이 선행한다. 그러므로 세계가 존재하지 않았던 시간 즉 공허한 시간이 선행해야 한다. 그러나 이제 공허한 시간 속에 어떤 사물의 발생도 가능하지 않다. 왜냐하면, 그 같은 시간의 어떤 부분도 다른 부분 앞에서 비 현존의 조건에 앞서 구별된 현존의 조건을 가지지 않기 때문이다. 그러므로 세계 속에서 사물의 많은 계열이 시작할 수 있지만, 세계 자체는 시초를 받아들이지 않는다. 세계는 지나간 시간과 관계하여 무한하다.”(칸트 재인용, 논리학 재판, GW21, S.231)

이 증명은 사물의 발생이 시간 속에 현존하는 조건을 갖는다는 것을 전제로 한다. 그런데 만일 아무것도 없는 공허의 시간에는 사물의 발생할 조건이 존재하지 않으니 사물이 발생하려면 시초 앞에 시간에도 사물이 있어야 한다. 결국, 세계의 시초는 있을 수 없다는 것이다.

그러나 사물이 반드시 그 앞에 발생 조건을 가질 필요가 있는가? 아무 조건 없이 출현하는 사물도 있지 않을까? 그렇다면 시초 앞에 공허한 시간이 있어도 무방하지 않을까? 헤겔은 이런 생각 끝에, 칸트의 증명이 정립에 대한 증명과 마찬가지로 증명돼야 할 것을 전제하고 있다는 것이다.

즉 여기서는 발생 조건이 전제되는데, 이 발생 조건이 있다는 것 자체가 시초가 없다는 것과 같은 말이 된다. 시초가 없다는 것이 증명돼야 하는 과제인데 이미 발생 조건이라는 말 속에 함축적으로 전제되고 있다.

이어서 칸트는 공간에 한계가 없다는 주장을 증명하는데, 이 증명은 시간의 무한성 증명과 같은 논리를 반복한다. 즉 사물의 공간이 한계가 있다면, 그 밖은 공허한 공간이어야 한다. 그러면 공허한 공간 속에 사물의 공간이 들어 있다는 것이다.

앞에서 시간의 무한성 증명에서는 조건이라는 개념이 이용됐다면 공간의 무한성 증명에는 관계 개념이 이용된다. 어떤 것이 공허와 관계한다는 것은 말이 되지 않는다. 존재하지 않는 무와 관계할 수는 없기 때문이다. 그러므로 관계가 있으려면 공허가 아니어야 하고 사물의 공간은 다시 더 큰 사물 공간 안에 들어 있어야 한다. 결국, 사물의 공간에는 한계가 없다는 것이다.

앞에서 발생 조건을 전제하는 것이 시간 앞의 시간을 전제하는 것과 같다고 했는데, 여기서도 마찬가지다. 공간의 관계를 전제로 하면, 이미 공간 너머 공간을 전제하는 것과 같으니, 여기서도 마찬가지로 증명돼야 할 것이 미리 전제된다고 하겠다.

시공간이 유한하다거나 무한하다는 중장은 동시에 성립하지 않으니, 칸트는 이를 이율 배반이라고 주장한다. 칸트는 이런 이율 배반이 나오는 이유는 사유의 범주, 판단의 형식을 경험적 개념에 적용하지 않고 물 자체의 개념 즉 시간, 공간, 우주, 세계와 같은 물 자체의 개념에 적용했기 때문이라고 본다. 그러므로 칸트는 이런 물 자체에는 유한성이나 무한성과 같은 사유의 범주를 적용하지 말아야 한다는 결론에 이르렀다.

그러나 헤겔은 칸트의 이율 배반을 비판하면서 거꾸로 말하자면 유한성과 무한성이라는 주장이 시간과 공간에 동시에 적용될 수 있다는 점에 주목한다. 그것은 곧 양적인 관계 즉 일자와 일자의 관계가 연속적인 동시에 불연속적이라는 이중적 성격을 지닌 한 불가피하게 나오는 것이다. 연속적인 동시에 불연속적이라는 것은 곧 한계가 자기를 자기가 넘어선다는 것을 의미한다. 이는 곧 어떤 정량은 자기 내에 무한성을 내포한다는 것을 말하는데, 헤겔은 칸트의 이율 배반을 비판함으로써 양적 무한성을 설명하려 했다.

헤겔은 칸트의 주장에 대해 이렇게 비판한다.

“세계에서 모순을 제거하고 반대로 모순을 정신 속으로 또는 이성 속으로 옮기고 그 속에서 해결되지 않은 채로 존립시키는 것은 세계에 대해 너무나 나약한 태도다. 사실상 정신은 모순을 견딜 수 있을 만큼 강력하며 그러나 또한 모순을 해소할 줄도 알고 있다. 그러나 소위 세계는 어디에서도 모순이 없지 않으며 모순을 견딜 수 없고 그러므로 생성과 소멸에 희생된다.”(논리학 재판, GW21, S.232)

세계의 모순을 인정하고 그것을 넘어서려는 분투의 정신이 여기에 표현돼 있다.

[특별기고] 헤겔 정신현상학의 시대적 의의 [흐린 창가에서-이병창의 문화비평]

2025년 11월 28일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 정신현상학의 시대적 의의

이 글은 『정신현상학 번역과 주해』의 발간을 기념해서 2025년 11월 27일 대안연구공동체(CAS)에서 진행 강연의 원고입니다.

강의영상은 아래 대안연구공동체 해당 게시물 링크로 접속하시면 보실 수 있습니다.

https://cafe.naver.com/paideia21/19183

글: 이병창(한철연 회원)

1) 필자의 관심

필자는 본디 인간의 마음을 이해하는 데 관심을 가졌다. 대학 시절 실존철학이나 불교에 깊이 빠졌던 것도 그 때문이었으리라. 필자가 문학과 예술에 늘 마음을 빼앗겼던 것도 그 속에서 다양하고 복잡한 인간의 마음을 엿볼 수 있었기 때문이었다. 철학과 대학원에 들어갔을 때도 실존철학을 연구하고 싶은 마음에서였는데, 어느 날인가 철학 하는 선배의 석사학위 논문을 읽다가 갑작스럽게 방향을 바꾸어 헤겔의 『정신현상학』을 읽기 시작했다. 그 논문의 주제는 『정신현상학』 자기의식 장에 나오는 주인과 노예의 관계였을 것이다.

그렇게 시작한 연구가 끝나지 않았다. 『정신현상학』은 도대체 이해되지 않았으니 처음엔 그저 한 쪽을 읽다가 잠에 빠졌으며 읽기를 매번 다시 포기했다가 얼마 뒤 다시 되돌아오기를 반복하면서 이제 70대 노인이 돼버렸다. 그간 몇 권에 걸쳐 『정신현상학』의 비밀을 풀어보려 했으나 다들 중도에 그치고 말았다.

두서너 해 전 코로나가 창궐하던 시대, 문득 죽음이 부르는 듯한 환청처럼 듣고, 죽기 전 마지막 힘을 다해 이 책의 번역과 주해를 마쳐야 하겠다는 생각으로 만사를 제치고 집에 틀어박혔다. 생각해 보면 학자적 삶의 거의 전부를 『정신현상학』의 이해에 매달렸으니, 무엇이 필자를 이 책에 걸신들리게 했는지를 이제 되돌아보지 않을 수 없다.

필자가 헤겔의 『정신현상학』에 몰두했던 것도 이 책이 본래 필자의 관심 영역인 마음의 문제를 다루었기 때문이다. 마음 즉 정신이란 단순히 세계에 대한 인식이나 삶의 가치를 다루는 것이 아니라 심성 즉 실천적 의지나 정신적 표현의 문제까지 포괄하는 개념이다. 많은 철학은 마음을 다루더라도 주로 인식과 가치의 문제만을 다룰 뿐이고 심성의 문제나 표현의 문제는 심리학이나 교육학 또는 예술의 문제로 넘겨버렸다. 심리학이나 교육학은 경험적 방법이나 실용적 목적이 지배하고 심층적 이해는 없었다. 예술은 표현을 개인의 천성의 문제로 돌렸으니 아쉬웠다. 일부 철학(예를 들어 실존철학)은 심성의 문제를 다루기는 했으나 적절한 방법론이 없이 내적인 수련의 문제로 여길 뿐이었기에 그 역시 필자로서는 답답했다.

그런 마당에 헤겔의 『정신현상학』에서 인식과 가치뿐만 아니라 심성이나 표현의 문제를 다룰 수 있는 학문적 방법론을 발견할 수 있었으니, 필자로서는 흥분하지 않을 수 없었다. 더구나 『정신현상학』을 조금씩 이해해 나가면서 그 가운데서 인간의 실천적 의지나 정신적 표현에 관련된 다양한 모습을 발견하게 됐다. 여기서 상세하게 설명할 여유는 없지만, 그 이름만 들어보자면 자기의식 장에 나오는 ‘노예 의식’과 ‘불행한 의식’이라든가, 이성 장에 나오는 ‘덕성’과 ‘세속’의 개념, ‘성실한 의식’ 그리고 정신 장에 나오는 ‘인륜적 의식’ ‛세계의 주인’ ‘소외된 정신’ ‘분열된 의식’이나 ‛순수 의식’ ‘유용한 존재’ ‘절대적 자유’ ‛전치[Verstellung]’와 ‛아름다운 영혼’의 개념 등이 있다. 헤겔은 많은 문학 작품이나 종교적 형태에서 그런 모습의 원형을 찾으려 했다. 그가 참고했던 대표적인 소설만 들더라도 소포클레스의 『안티고네』나 디드로의 『라모의 조카』, 야코비의 『볼데마르』 등이 있다. 그 모습은 필자가 기대했던 것 이상으로 풍요로웠으니 그 모습을 발견할 때마다 필자로서는 놀라움을 금하지 못했다.

헤겔은 그 모습을 역사적으로 출현하는 것으로 설명했다. 그것은 과거의 모습을 극복하는 한에서 출현하며, 출현했다가는 역사적 운동을 거쳐 다시 자기 모순에 빠지고, 그럼에도 새로운 극복의 가능성을 열어준다. 그 모습은 한편으로 보면 역사 앞에서 부딪히는 모순 때문에 비극적으로 몰락하면서 숭고성을 띤다. 그러나 다른 한편 현실의 역사를 은폐하려는 시도 속에서 풍자되고 희화화된다.

2) 정신현상학의 역사적 배경

그런데 헤겔이 정신현상학을 쓰게 된 동기는 무엇일까? 필자는 그 동기를 두 가지 측면에서 바라볼 수 있으리라 생각한다. 하나는 그 시대 역사적 배경이며 여기서 정신현상학이 추구하는 목표가 나온다. 다른 하나는 철학적 배경인데 여기서 정신현상학이 전개되는 구조와 전개 방식이 나온다.

① 독일의 궁핍

우선 그 역사적 배경을 살펴보자. 헤겔 시대 이웃하는 영국이나 프랑스에서는 이미 민족적 통일 국가와 근대적 민주주의 체제 그리고 활발한 자본주의적 발전이 일어나고 있었다. 그러나 독일은 여전히 중세 봉건적 시대를 벗어나지 못했다. 17세기 초 30년 전쟁이 끝난 뒤 독일은 소 국가로 분열됐으며, 각 국가는 봉건적 지배 아래 있었고 자본주의적 발전은 오히려 후퇴하고 말았다.

그런 상황에서 프랑스 혁명의 기운을 전해 받고, 나폴레옹의 지배 아래 프로이센을 중심으로 일부 개혁이 이루어지면서 독일에서도 혁명적 지식인이 출현했다. 헤겔 역시 이 시대 청년기를 보냈으며, 그런 혁명적 지식인의 이상을 공유했다. 그러나 다른 한편 청년들은 프랑스 혁명 가운데 전개된 공포 정치에서 충격받았으며, 새로이 발전하는 자본주의의 불평등을 목격했으니, 혁명적 지식인들은 한편으로 근대적 체제를 실현하면서도 다른 한편으로 공포와 불평등이 없는 이상을 실현하려 했다.

② 헨 카이 판의 이념

그것이 곧 헨 카이 판[hen kai pan]이라는 이념이었다. 이것은 곧 ‘하나이자 전체[All Einheit]’라는 사상을 구체적으로 실현한 것이다. 이 원리는 그리스 헤라클레이토스의 단편에서 나온다고 하는데, 헤겔은 청년기부터 시인 횔덜린과 자연철학자 셸링과 더불어 가슴에 품고 있었다고 하는 원리다. 이 원리를 헤겔은 각자는 전체이면서 동시에 전체의 한 계기라는 의미로 재해석한다. 필자는 이를 간단히 공동체적 정신이라고 부르려 한다.

그런 이상의 가능성 보여준 최초의 인물이 곧 칸트였다. 칸트는 로베스피에르가 사사한 루소의 일반 의지 개념이 지닌 한계를 깨닫고 이를 극복하기 위해 순수 의지 즉 도덕적 자유의지 개념을 제시했으니, 칸트의 세례를 받은 청년 지식인들은 이런 도덕적 자유의지를 통한다면 자신의 이상을 실현할 수 있다는 희망에 들뜨게 됐다.

그러나 칸트의 순수 의지 개념은 나름대로 문제를 지녔으니, 이 문제를 극복하기 위해 낭만주의자는 이를 양심 개념으로 발전시켰으며, 헤겔은 그것조차 넘어선 ‘하나이자 전체’라는 절대지의 개념을 제시하기에 이른 것이다.

헤겔은 정신현상학 서문에서 칸트 철학에서 새로운 빛이 탄생했다고 한다. 이 빛은 철학적으로는 선험철학이며 사상적으로는 그의 순수 의지 개념이다. 칸트는 이런 순수 의지가 지닌 자체 내 한계 때문에 낭만주의의 양심 개념이 출현했다고 한다.

③ 낭만주의의 한계

헤겔은 낭만주의적 양심 개념을 정신현상학의 절대정신에 도달하기 직전에 다루었는데, 그만큼 그가 중요하다고 생각하기 때문이었다. 그러면서도 결정적 한계를 지니고 있었는데 그것은 그 시대 낭만주의자들이 나갔던 길을 보면 충분히 이해될 것이다.

독일 낭만주의는 여러 흐름이 있지만, 대체로 학생운동을 배경으로 한다. 이 학생운동은 예나 대학에서 시작돼서 전국적으로 파급됐다. 학생들은 학생조합이라고 할 부르셴샤프트를 조직해서 활동했는데, 초기에는 매우 급진적이었다. 학생운동은 독일의 통일과 민주화를 요구했다. 그러나 1807년 나폴레옹의 독일침략을 거치면서 학생운동은 분열했다. 상당수는 보수화했다. 그들은 종교적으로 개신교에서 가톨릭으로 전향했고 정치적으로는 민족주의적으로 전향했다. 그런 가운데 중세를 이상화했고 신성로마제국의 부활을 꿈꾸었으며 그 후예라고 할 합스부르크의 오스트리아 제국을 지지했다. 반면 급진파는 전쟁 이후 1814년 발트부르크 축제를 통해 보수파의 저서를 불태우는 등 급진적인 활동을 전개했다.

이렇게 낭만주의 운동은 급진파와 보수파로 분열된 가운데 온건 개혁파라고 할 프로이센 중심의 독일 개혁 운동을 반대했다. 여기서 정치적으로나 사상적으로 낭만주의와의 대결이 전개됐는데, 이때 헤겔은 낭만주의의 양심 개념이 지닌 긍정적 측면과 부정적 측면을 동시에 보면서 이를 극복해야 할 필요성을 느끼게 됐다. 바로 이것이 그가 사상적으로 절대정신으로 이행하게 된 역사적 동기였다고 하겠다.

3) 정신현상학의 목적

헤겔은 이념적으로는 낭만주의자들이 지닌 이념을 지지했다. 그 역시 헨 카이 판의 공동체를 지지했으며 이를 통해 독일의 봉건제와 민족적 분열, 자본주의적 참상을 극복하고자 했다. 그러나 그 방법에서 그는 칸트의 순수 의지도 아니고 낭만주의의 양심도 아니며 그것을 넘어선 절대정신을 요구했는데, 그렇다면 절대정신이란 무엇인가?

헤겔에서 절대정신이란 곧 공동체다. 이 공동체는 단순히 공동의 목적(이성, 법)을 의미하지 않는다. 이 공동체는 그와 동시에 개별 의지의 통일체 즉 집단의지 또는 공동 자아를 말하며, 이는 국가라는 형태로 드러난다. 다음 구절을 참조하라.

“절대정신은 곧 공동체다. 이 공동체는 우리가 이성이 실천적으로 실현된 형태로 들었을 당시에는 우리에게 절대적 본질로 나타났으나 여기서는 자신의 진리에 도달하면서 자기 자신에 대해 의식된 인륜적 본질 즉 우리가 대상으로 삼는 본질로 등장한다.”(446 구절)

이런 절대정신은 구체적으로 두 가지 모습을 지닌다. 하나는 내적인 모습인데 그것은 사랑이라는 정신으로 출현한다. 이는 근대에서 개신교를 통해 출현했다. 다른 하나는 외적인 모습인데 앞으로 구체적으로는 국가로 출현해야 할 이상이다. 이는 곧 사랑이 현실적으로 실현될 수 있는 사회 제도를 의미한다.

헤겔은 이 사회 제도를 나중에 법철학에서 제시했는데 이는 기독교의 삼위일체라는 개념에 기초해서 전개된 것이다. 즉 국가가 삼위일체와 같은 방식으로 구성되는 것을 말한다. 삼위일체는 각각이 전체이면서 동시에 전체의 한 계기라는 헨 카이 판의 원리에 기초하지만, 개별자와 일반자 사이에 양자를 매개하는 특수자를 개입시켜 세 가지 항이 각기 전체이면서 동시에 전체의 한 계기가 되도록 만든 것이다. 국가 속에서 이런 삼위일체의 방식을 구체적으로 어떻게 적용하는가는 법철학에서 나오지만, 여기서는 생략하도록 하자.

정신현상학에서 중요한 것은 어떻게 이런 절대정신에 도달할 수 있는 가이다. 헤겔은 이와 같은 절대정신에 추상적인 윤리적 사유가 아니라 역사를 통한 실제 훈련을 통해 몸으로 직접 체득할 수 있으리라고 생각했다. 그러면서 그는 구체적으로 역사 속에서 이런 절대정신에 도달하는 길을 찾으려 했으니, 바로 이것이 정신현상학이 정신의 역사로 구성된 이유다.

4) 정신현상학의 철학적 배경

그렇다면 역사 속에서 정신이 어떻게 전개되는가? 여기서 헤겔은 정신이 전개되는 구체적 방식에 대해 고민하게 되는데, 이런 고민은 그 시대 철학적 문제와도 관련된다.

① 의식 경험의 길

『정신현상학』이 전개되는 방법은 헤겔이 「서론」에서 ‛의식 경험의 길’이라는 개념을 통해 밝혔다. 이 개념은 칸트의 선험철학에서 출발한다. 그것은 곧 대상이란 의식의 범주가 규정하는 것이라는 관점이다.

이런 관점에 서면 의식의 경험은 대상 너머에 있는 물 자체에 부딪히게 된다. 이는 곧 의식의 범주로 규정되지 않는 딜레마나 모순이 출현한다는 것을 의미한다. 칸트 철학은 이런 물 자체에 부딪힘으로써 그 너머 영역은 인식 불가능한 영역으로 규정했다. 이 물 자체의 난제를 해결하는 것이 시대의 과제였다. 직관으로 돌아간 셸링과 달리 헤겔은 칸트 선험 원리를 지키면서도 이 물 자체의 난제를 해결하고자 했다. 헤겔은 여기서 의식 경험의 개념을 제시한다.

헤겔에 따르면 의식 경험의 길에서 딜레마나 모순을 통해 드러나는 물 자체는 사실 그 의식이 이미 전제한 특정한 범주를 통해 대상을 규정하는 것 때문이다. 그런 특정한 범주를 벗어나게 되면 더는 딜레마나 모순이 출현하지 않게 된다고 주장한다. 그는 이런 딜레마나 모순에 부딪히면 의식은 자기 내로 반성하여 기존의 의식 형태와 다른 새로운 의식 형태가 출현하며 이를 통해 의식이 자기 내로 반성하는 것이 곧 헤겔이 말하는 의식 경험의 길이다.

의식의 자기 내 반성은 그 의식에 대해 존재하는 대상을 넘어 물 자체 즉 딜레마가 출현하는 것을 매개로 한다. 의식이 딜레마를 매개로 더 일반적 의식으로 발전하면서 기존의 물 자체는 의식이 파악하는 현상 영역 안으로 들어오고, 이에 따라 의식이 규정할 수 있는 대상의 영역도 확장된다. 하지만, 이 새로운 의식 경험 역시 일정한 범주를 전제로 구성된 것이니, 다시 물 자체에 부딪히게 된다. 이렇게 매번 새롭게 등장하는 물 자체는 이전에 출현했던 물 자체보다 더 근본적인 물 자체가 될 것이다.

② 근거로의 복귀와 개념의 실현

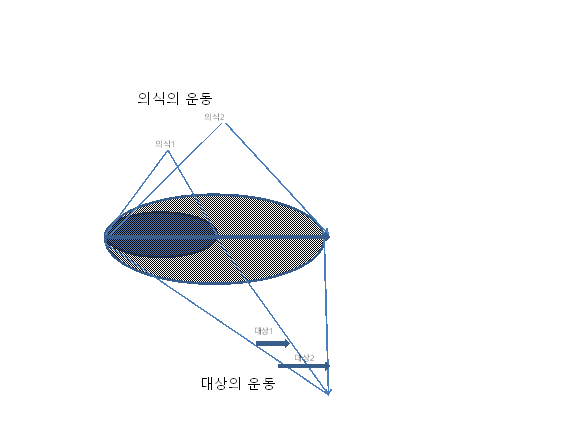
이와 같은 ‘의식 경험’의 개념에 따르면, 의식은 개별적 형태에서 일반적 형태로 발전한다. 즉 좁은 영역에만 적용되는 의식의 범주는 이로부터 발생하는 물 자체까지 포괄하는 더 넓은 영역에 적용되는 일반적 의식 범주로 발전한다. 개별적 의식에 대해 일반적 의식은 근거가 되는 것이므로 의식 경험의 운동은 자기 내에 있는 근거로 복귀하는 운동이라 할 수 있다. 이 운동은 의식이 물 자체라는 대상에 부딪히는 운동이며, 마침내 의식과 대상이 통일되면서 자기의식이 되는 운동이다.

의식의 이런 운동은 출발점에서 본 운동이다. 이 운동을 그 결과에서 그리고 대상의 측면에서 본다면, 결과는 더 포괄적인 대상이므로, 이런 대상이 의식의 출발점에 가능성으로 있다가 마침내 실현된 것으로 볼 수 있다. 이런 측면에서 운동은 추상적이며 가능적인 것에서 구체적으로 실현된 것으로 나가며, 헤겔은 이런 운동을 개념의 자기실현 운동이라 한다. 여기서 추상적 가능성을 헤겔은 그 자체 존재라고 하고 이 그 자체 존재는 자기 밖의 물 자체에 대립하게 되면, 대자 존재와 대타 존재로 분리된다. 그리고 최종적으로 구체적으로 실현된 것을 그 자체이면서 동시에 대자적인 것이라 한다.

——————–

여기서 의식의 반성과 대상의 출현이 서로 매개한다. 의식이 자기 내로 발전하는 과정은 거꾸로 보면 대상의 본질이 드러나는 과정 즉 물 자체가 출현하는 과정을 매개로 한다. 거꾸로 대상의 본질이 드러나는 과정은 의식의 자기 내 반성을 매개로 한다. 의식이 더 일반적 의식이 되면서 더 근본적인 대상의 본질이 출현하게 된다.

————————-

의식이 존재하는 한, 끝없이 그 의식을 넘어서 규정될 수 없는 물 자체가 출현할 것이니 이 과정은 개방적이고 열린 과정이라 할 수 있다. 그러나 일정한 시대에서는 더는 당시의 의식으로 규정되지 않는 대상은 없으니, 그런 한에서 이 과정은 닫힌다. 열림과 닫힘은 서로 교체된다. 열린 운동 끝에서 보면 닫힌 것이며, 닫혔다 하더라도 새로운 물 자체가 출현하면, 다시 열리게 된다.

의식의 경험에서 의식은 개별적 의식에서 일반적 의식으로 발전한다. 반면 대상의 실현은 추상에서 구체로 나가니, 양자는 서로 전도된 모습을 취하고 있다. 전자가 상향적이며 끊임없이 자기를 넘어서는 개방적 과정이라면 후자는 하향적이다.

의식 운동이나 개념 운동은 서로 매개하는 것이니, 의식 운동의 이면에 개념 운동이 있으며, 개념 운동의 이면에 의식 운동이 있다. 헤겔의 경우 대부분 학문은 개념 운동의 길을 택하고 있다. 학문의 경우(논리학이든 자연철학이나 정신철학이든) 개념 운동이 전면에 나오며 그 이면에 의식 경험이 전개된다. 반면 『정신현상학』의 경우는 의식 경험의 길이 전면에 나오며 그것을 매개하는 것이 대상의 개념 운동이다.

———————–

마르크스는 헤겔이 말한 의식 운동과 개념 운동을 연구 과정과 서술 과정으로 설명했다. 연구 과정은 경험적으로 얻어지는 개별 사실들에서 출발하여 가장 일반적이고 근거가 되는 원리로 나간다. 서술 과정은 연구 과정을 통해 발견된 원리로부터 시작한다. 여기서 추상적 원리를 구체화하면서 현실의 대상을 설명하게 된다. 마르크스의 경우에서도 연구 과정과 서술 과정이 서로 매개한다. 마르크스의 자본론을 보면, 장마다 먼저 개념적으로 서술한 다음 이를 다시 역사적인 발전을 덧붙이는데, 이는 연구 과정과 서술 과정이 매개됨을 보여준다.

③ 형태와 계기의 운동

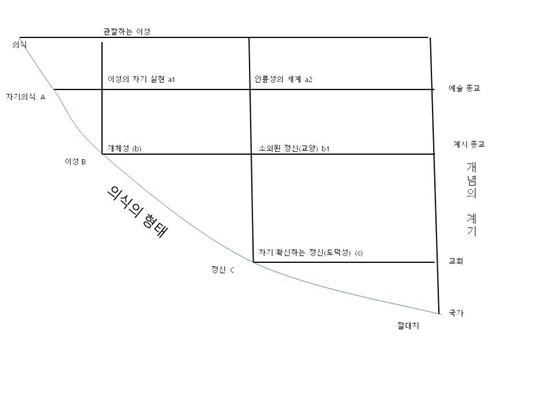
의식이 전개되는 과정에서 이전의 의식 형태는 이후의 의식 형태에 내면화[기억:Erinnerung ]되니, 이후의 형태가 전개될 때는 이전의 형태가 다시 반복된다. 다만 과거의 것이 똑같이 반복되는 것이 아니라 새로운 의식 형태를 지반으로 해서 반복된다. 그러므로 헤겔은 이를 개념의 계기가 된다고 한다. 의식 형태의 이행은 개념의 계기가 전개되는 과정에서 반영된다. 전자는 시간 속에서 일어나며, 이것이 곧 의식 경험의 길이다. 후자는 논리적 과정이며 이것은 앞에서 말한 대상의 개념 운동과 같은 것이다. 시간 속에서 이행과 사유 속에서 이행은 서로 다른 차원에 놓여 있음에도 서로 평행한다. 양자의 과정은 마치 계통의 발생 과정을 개체가 반복하는 것과 같다. 헤겔은 이를 형태와 계기의 관계라고 한다.

5) 정신의 전개 과정

헤겔에서 정신은 매우 포괄적인 개념이다. 이 정신은 세 가지를 포함한다. 즉 인식과 실천적 의지 그리고 표현이다. 헤겔은 『정신현상학』에서 이 세 가지 영역을 개별성과 일반성이라는 두 단계로 구분해서 다룬다. 그러므로 전체적으로 보면 『정신현상학』은 다음과 같이 구성된다. 이 구성은 대체로 헤겔이 칸트의 범주표에서 끌어낸 4개 범주(12개 판단형식)에 대응한다.

정신현상학	내용		판단형식
의식	개별적 인식	개별자의 본질을 인식하려는 시도가 다루어진다.	질 범주
자기의식	개별적 의지 (자아)	형식적 자유의의 출현 과정이 탐구된다. 이는 노예의 노동을 통해서 내적으로 출현하고 스토이시즘과 회의주의 불행한 의식을 거쳐 현실적으로 출현한다.	양(본질) 범주
이성	일반적 인식	사물의 일반적 본질이 인식된다. 이는 자연에서는 분류학의 형태로 출현하며, 인간 사회에서는 정의의 개념으로 출현한다.	실체 범주
정신	일반적 의지 (일반적 자아)	개별 의지가 자기를 극복해서 일반적 본질 즉 정의를 실현하려는 이성적 의지로 발전하는 과정이 다루어진다. 이 과정에서 계몽주의, 프랑스 혁명, 칸트의 자유의지, 낭만주의의 양심 개념 들이 다루어진다.	개념 범주
절대정신	정신의 표현 (예술, 종교, 철학)	정신의 표현은 개별 의지를 공동 자아로 조직하는 방식을 결정한다. 그 공동 자아는 종교에서는 교회라는 형식으로 나타나며, 절대지의 단계에서는 삼위일체적 이상 국가로 출현한다.	이념

이런 과정에서 자기의식의 단계에서 개별적 자유의지가 출현한다. 이는 곧 형식적으로 자유로운 의지, 결정하고 선택하는 의지를 말한다. 이성의 단계에서 사회의 공동 목표라고 할 정의가 파악된다. 그리고 정신의 단계에서 이런 공동의 목표를 수행하는 실천적 의지가 형성된다. 마침내 절대정신의 단계에서 이런 실천적 의지 가운데 공동체의 정신이 출현하면서 구체적으로 이상 국가의 출발점이 된다.

6) 정신현상학과 이 시대의 철학

마르크스는 역사가 반복된다고 했다. 한 번은 비극이고 다른 한 번은 희극이다. 마찬가지로 사상도 반복하는 것이 아닐까?

90년대 초 포스트모던 사상이 불어닥쳤다. 대체로 푸코, 데리다 등 포스트모던 사상가는 후기 구조주의에 기초한다. 포스트모던 사상은 진리도 부정하고 어떤 가치도 부정한다. 포스트모던 사상은 억압을 반대한다는 긍정적 가치도 지니지만, 모든 것을 상대화하고 결국 개인주의, 상업주의, 쾌락주의를 정당화해 왔다. 이는 이 시대 함께 퍼진 신자유주의 체제의 이데올로기로 작동했다.

2008년 세계 금융위기를 전후로 신자유주의가 비틀거리기 시작했다. 이와 더불어 포스트모던 사상의 상대주의를 극복하려는 시도가 전개됐고 그 결과 전 세계적으로 직관주의적 철학이 발전했다. 라캉은 이드를 직접 대면하는 순간이 있다고 보았으며, 들뢰즈는 사물을 생성하는 미분적 차이를 직관할 수 있다고 보았다. 직관주의는 포스트모던 시대 사라진 진리와 객관적 가치를 찾으려는 숭고한 노력이었으나, 직관 개념이 지닌 한계를 벗어나지 못한다. 직관은 결국 주관적이기 때문이다.

21세기를 수놓은 이런 사상의 발전은 거슬러 올라가면 헤겔 당시의 사상사적 발전을 상기시킨다. 칸트의 선험철학은 구조주의와 유사하다. 이어서 등장한 낭만주의 철학은 직관주의다.

헤겔은 칸트 선험철학을 계승한다. 즉 사태를 인식하는 데서 개념의 구조를 전제한다. 그렇게 된다면, 칸트가 말했듯이 물 자체의 아포리아에 부딪히고, 상대적 현상주의에 빠지게 되지 않을까? 그러나 헤겔은 개념의 구조를 전제하면서도 진리와 객관적 가치의 인식에 육박할 수 있다고 하면서 상대주의를 극복할 수 있다고 보았다.

그러면서 그는 개념을 거부하고 직관에 의존해 진리를 인식하려는 낭만주의를 비판했다. 즉 진리를 회복하려는 낭만주의의 이념을 받아들이면서도 그 방법에서 헤겔은 직관이 아니라 구조적인 개념을 통해 가능하다 보았다. 그 과정에 곧 앞에서 말한 의식 경험의 길인데 즉 모순과의 대결을 통해 사유가 객관화된다는 것이다. 그런 의식 경험의 길을 통해 헤겔은 한편으로 자기가 진리다라고 주장하는 독선적 오만에 빠지는 것도 경계하면서 다른 한편으로는 진리를 포기하고 상대적 세계에 머무르는 것도 거부한다. 헤겔은 신이 아닌 인간으로서는 모순에 온 몸으로 부딪혀 가면서 진리를 향해 끊임없이 전진하는 고투 외에 다른 길이 없는 것으로 주장한다고 할 수 있겠다.

헤겔이 제시하는 정신적 고투를 가장 잘 보여주는 것이 아인슈타인의 물리학이 뉴턴의 물리학을 포함하면서도 넘어서는 것이거나 마르크스가 정치경제학의 노동 가치설을 수용하면서 이를 넘어서 독자적인 가치론을 확립한 것에서 발견할 수 있지 않을까?

헤겔 형이상학 산책50-양적 무한성 [흐린 창가에서-이병창의 문화비평]

2025년 11월 28일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책50-양적 무한성

앞에서 셈법과 수의 종류를 다룰 때 정수에서 분수로 이행하면서 새로운 양이 출현한다고 했다. 정수는 외연 량을 표현한다. 그것은 길이나 무게와 같은 추상적인 개별 량이다. 분수는 비례 량을 표현한다. 이것은 두 개의 서로 다른 정량의 관계로 이루어진다. 예를 들어 무게와 부피의 비례인 비중, 거리나 시간의 비례인 속도와 같은 것이다. 이런 관계를 통해 성립하는 구체적인 양을 비례 량이라고 이름 붙였다. 양자를 매개하는 것이 내포 량 또는 정도다. 내포 량은 타자와 비교에서만 성립하지만, 여전히 추상적인 양이다.

외연 량(정수)에서 비례 량(분수)으로 나가는 과정은 경험적으로는 경험이 더 풍부해져서 개별적 정량을 넘어선 다른 정량들 사이의 관계가 출현했기 때문이다. 그런데 헤겔은 이런 이행을 추상에서 구체로 나가는 개념의 실현 운동으로 설명한다.

이 운동 과정에 대한 헤겔의 설명은 모호하다. 이는 c절 양적 무한성 절에서 설명되는데, 표면적으로 보면, ‘악 무한’에서 ‘진 무한’으로 이행하는 것으로 설명된다. 그 사이를 매개하는 것이 무한 진행이다. 무한 진행이 악 무한(예를 들어 무한대나 무한소)으로 표현됐다가, 이것이 무한 진행임이 밝혀지고 나아가서 그 본질은 진 무한 또는 내적인 무한성 개념이라는 사실이 자각된다.

처음 악 무한을 다룰 때는 헤겔의 설명은 동일한 정량에서 정량의 운동(예를 들어 길이의 확장)을 설명하는 듯이 보였다. 그런데 진 무한 개념이 등장하면서 이 진 무한이 곧 비례 량 즉 다른 정량의 내적 관계임을 천명하면서 끝난다. 이 과정은 약간 어리둥절하게 보이며 이 과정을 분석적으로 이해하기가 쉽지 않다. 그러나 여기에 헤겔이 논의를 전개하는 독특한 방법이 숨어 있지 않을까 생각한다. 이제 헤겔의 논의를 따라가 보자.

먼저 헤겔에서 양적 무한성에 관한 개념을 확인할 필요가 있다. 그 출발점은 하나의 정량과 다른 하나의 정량이 관계다. 이 관계는 길이나 무게와 같은 개별 정량에서 두 정량의 관계로 볼 수도 있고 비중같이 두 다른 정량 사이의 관계로 볼 수 있다. 차라리 헤겔의 개념 규정은 앞으로 보게 되겠지만, 이 두 차원을 넘나든다고 할 수 있다. 여기서는 개별 량와 비례 량이라는 구체적 내용의 차이를 무시하고 두 정량의 일반적 형식적 관계를 보자.

양적인 것은 대자 존재인 일자에서 동일한 대자 존재인 다른 일자로 이어지는 것이다. 여기서 서로 같은 대자 존재가 관계한다는 점에서 연속적이며 각 대자 존재는 고유한 일자라는 점에서 서로 구별되고 무차별하므로 이 관계는 분산적이다.

양적 관계가 이와 같은 이중성을 지니므로, 어떤 정량의 부정은 정량의 타자지만 또 하나의 정량이 된다. 그러므로 그 부정은 새로운 정량에 머무르지 못하며, 그 새로운 정량조차 자기를 부정하게 하니, 이 과정은 끝없이 계속된다. 새로운 정량은 기존 정량의 부정이면서 동시에 자기가 부정되니, 이중 부정 또는 자기 부정이며 이런 점에서 무한 정량, 즉 양적인 무한성이 된다.(이런 자기 부정성 개념은 길이나 무게 등 개별 정량의 무한 진행에서 잘 드러날 것이다.)

앞에서 질적 무한성 개념을 다룰 때도 양적 무한성에서와 마찬가지의 자기 부정성이 출현했다. 그러나 같은 자기 부정성이더라도, 질적 무한성과 양적 무한성에서 나타나는 모습은 다르다. 이제 현존 절에서 다루었던 질적 무한성과 양 절에서 나타나는 양적 무한성을 비교해 보자.

질적 존재에서 규정성은 어떤 것이 지닌 속성이다. 예를 들어 소금은 짜거[p]나 입방체[-p]다. 모든 소금은 짜며, 동시에 입방체다. 양자의 통일은 p가 아니고 -p도 아니며 동시에 p이면서 -p인 것이다. 이것은 서로 대립하는 p와 -p를 매개하고 자기를 p와 -p로 출현하게 하는 동시에 양자를 초월하는 일반성 즉 대자 존재다.

이 질적 무한성 즉 대자 존재는 자기를 때에 따라 p나 -p와 같은 대립하는 성질로 나타내는 운동을 의미하지만, 그 자신은 질적 성격을 잃어버리고 양적인 것으로 전환한다. 왜냐하면, 대자 존재와 대자 존재는 일자와 일자의 관계이며 양적인 관계이기 때문이다. 즉 질적 무한성은 양으로 이행한다.

일반적으로 질적 규정성은 타자와 대립하는 가운데 타자의 부정을 통해(반성적으로) 규정된다. 예를 들어 짠맛은 입방체에 대립해서 짠맛으로 규정된다. 즉 p는 -(-p)이다. 양적인 것에서는 이런 타자에 대한 대립 관계가 사라진다. 그 때문에 질적 성격도 사라진다. 여기서는 동일한 대자 존재 그러나 서로 무차별한 존재 즉 일자와 일자 사이의 관계만이 존재하기 때문이다.

그런데 양적 존재에서 두 대자 존재, 즉 일자와 일자는 서로 동일한 것이면서도 서로 무차별한 것이다. 두 개의 나뭇잎, 두 개의 물방울은 서로 무차별하면서도 서로 동일하다. 그러므로 여기서 양적인 무한성 즉 p가 아닌 것은 그 자체가 p이므로 자기 자신도 부정할 수밖에 없으니 어떤 부정은 자기 부정으로 나타나게 된다. 이런 끝없는 자기 부정성이 곧 양에서 나타나는 양적 무한성이다. 이런 양적 무한성은 하나의 정량 내에서 이 정량이 자기를 부정해서 자기를 넘어서게 만드는 것 그러므로 내적인 무한성이다.

그런데 여기서 우리가 주목해야 할 것은 정량에서 나타나는 자기 부정성이 독특하다는 사실이다. 정량의 자기 부정성은 어떤 정량의 타자가 곧 자기 즉 자기와 같은 대자 존재이므로 나타나는 자기 부정성이다. 그러므로 이 부정성은 타자를 부정해서 다시 자기가 되는 것이다. 전자의 측면에서는 타자로 미끌어지는 것(무한 진행)이며 후자의 측면에서는 자기 자신으로 되돌아오는 것이다. 미끌어진다는 측면에서 그것은 무한성이다. 그러나 타자를 부정해 자기로 돌아온다는 측면에서는 규정성이다. 질적 규정성이란 타자에 대립해서 나타나는 부정성을 의미하는 것이기 때문이다. 이렇게 해서 무한성을 통해 양에서 질적인 것이 회복된다.

예를 들어(이런 의미에서 양적 무한성은 개별 량에서보다 오히려 비례 량에서 더 잘 드러난다) 무게는 독자적인 정량일 수도 있고 부피에 비례하는 정량일 수도 있다. 후자가 비례 량이다. 전자일 때는 정량의 규정성(예를 들어 삼 미터)은 자기(길이)에 대해 외면적이다. 그 규정성은 자기에 무차별하다.

그러나 부피에 비례하는 무게 즉 밀도 또는 비중은 같은 타자에 대해 관계하는 정량이다. 비중이 크다는 것은 그저 무게와 무차별한 부피에 대해 무게가 외면적으로(사유를 통해) 비교된 것이 아니다. 비중은 부피라는 자기의 타자에 대해 관계하며 그것도 대립적으로 관계하니 즉 비중이 크다는 것은 자기의 부피를 축소한다는 것을 의미한다. 비중은 부피에 대립하고 부피를 부정하는 것이다.

이처럼 타자에 대립해서 규정되므로 질적인 규정성이 다시 회복된다. 비례 량을 이루는 구성 요소인 개별 양은 추상적이고 그 각각은 양적 관계를 갖지만, 비례 량에 이르면, 그 자체는 한편으로는 여전히 양적 관계에 머무르면서도 이제 질적 차이를 발생하게 한다. 이런 점에서 헤겔은 양적 무한성 즉 이중적 부정은 “어떤 정량으로서뿐만 아니라 정량 자체로서 지양된 정량이다.”(논리학 초판, GW12, S. 140)라고 한다. 즉 단순히 하나의 정량을 부정하는 것이 아니라 정량 자체를 부정하는 것 즉 질을 회복한다는 것이다.

“정량은 자기의 비 존재 무한자를 매개로 하여 다른 정량 속에서 자기 규정을 갖는다. 즉 질적인 차원에서 정량의 본성으로 된다. 그러나 정량의 개념과 그 현존을 비교하는 것은 차라리 우리의 반성에 속하며 즉 여기서 아직 출현하지 않은 비례에 속한다. … 이제 외면성 속[정량의 타자]에서 자기 자신이라는 것, 외면성 속에 자기 관계하며 자신과 단순한 통일성 속에 있고 질적으로 규정되어 있다는 것이 정립된다.”(논리학 재판, GW21, S. 235)

“이 비례 속에서 정량은 자기에 외면적이며 자기 자신과 상이하다. 그러나 이 자기의 외면성, 다른 정량에 관계하는 것이 동시에 그의 규정성을 이룬다. 이 속에서 무차별한 규정성이 아니라 질적 규정을 갖는다. 정량은 자기의 외면성 속에서 자기 내로 복귀한다.”(논리학 초판, GW12, S. 153)

양적 무한성의 개념은 이처럼 자기를 자기가 부정하는 것이라는 의미다. 그런데 헤겔은 양적 무한성 개념을 통해서 무한대나 무한소, 무한 진행, 진정한 무한성이라는 세 가지 개념을 구분한다.

무한대, 무한소는 무한히 크고 무한히 작은 것을 실체화하여 실제로 그런 것이 존재한다고 할 때다. 그것은 마치 피안이 존재한다고 할 때와 같은 의미다. 반면 무한 진행은 정량이 극한에 도달한 순간 다시 그것을 넘어가는 것을 말하니, 비유하자면 수평선을 끝까지 가면 다시 더 멀어지는 것과 마찬가지인 것과 같다.

그러나 헤겔은 무한대나 무한소는 잘못된 이미지라고 보며 이를 일단 무한 진행이라는 개념으로 환원한다. 사실 엄밀하게 말해서 무한대나 무한소는 실제로 존재하는 것은 아니다. 헤겔에 따르면 그것은 무한 진행의 왜곡된 표현이며 이 무한 진행을 일정한 이미지로 표현한 것에 지나지 않는다.

“무한대나 무한소로서 무한량은 본래 무한 진행이다. 그것은 크거나 작은 것으로서 정량이면서 정량의 비존재다. 따라서 무한대나 무한소는 표상을 이미지화한 것이다. 그 표상은 좀더 가까이 다가가 고찰해 보면, 무실한 그림자와 안개처럼 나타난다.”(논리학 재판, GW21, S. 233)

“정량을 넘어서는 것은 정량의 부정 즉 무한이다. 그러나 새로운 정량이 정립되면서 이것은 무한의 부정이다. 이 악 무한은 표상에서 절대자로 여겨지며 다시 지양되지 않는 최종적인 것으로 여겨지고 그것을 더는 넘어설 수 없는 것으로 여겨진다.”(논리학 초판, GW12, S. 151)

헤겔은 이런 무한 진행 역시 넘어서면서 이 무한 진행은 진 무한으로 이행해야 한다고 말한다. 무한 진행은 끝없이 자기를 부정해서 앞으로 나가는 운동인데, 진 무한은 자기를 부정하고 자기를 넘어서는 탈자화의 운동 자체를 말한다.

엄밀히 말하자면, 무한 진행와 진 무한은 다를 바가 없다. 둘 다 자기를 넘어서는 운동이다. 진 무한이라 할 때는 어떤 정량 속에 그것이 자기를 넘어서는 운동을 말한다. 무한 진행이라 할 때는 그런 진 무한의 운동한 결과 도달한 결과가 다시 넘어서서 끝없이 전개되는 것을 말한다. 진 무한이 내적 운동이라면 무한 진행은 그런 내적 운동의 표현이다.

자기를 부정한다는 것은 질적 무한성에서도 출현한다. 이때는 질적 무한성은 대립하는 성질을 넘어서는 포괄적 일반화로 즉 대자 존재로 나간다. 그러나 양적인 것의 평면에서는 자기 부정성은 즉 양적 무한성은 일반화가 아니라 옆으로 미끌어지는 무한 진행의 모습으로 나타난다.

그럼에도 무한 진행의 진정한 모습이 내적 부정성에 있다는 것을 깨닫지 못하고 그저 외면적으로 끝없이 앞으로 나가는 모습만을 취해서 본다면 그것이 헤겔이 비판하는 무한 진행이다. 무한 진행은 아직 내적 부정성의 운동임을 모르고 있는 내적 부정성의 운동일 뿐이다. 거꾸로 무한 진행이 지닌 본래적 모습을 자각한다면, 그것이 곧 진 무한이다. 헤겔은 이 진 무한을 ‘정량의 개념’, ‘개념에 따라서 규정된 정량’이라고 말한다.

“따라서 무한자는 다만 최초의 부정으로 규정되고 무한 진행 속에 나타난다. 그러나 이런 무한 진행 속에서 그 이상의 것이 출현한다는 사실이 지적되어 왔다. 즉 부정의 부정 또는 본래적으로 무한자인 것이 말이다. 이런 사실은 정량의 개념이 이를 통해 회복된 것으로 여겨져 왔다.”(논리학 재판, GW21, S. 234)

위에서 악 무한이나 무한 진행은 진 무한을 왜곡된 방식으로 표현하는 것으로 설명했다. 그러나 헤겔의 설명을 제대로 이해한다면, 사실 이런 무한의 여러 종류는 자연의 운동 또는 수 운동의 종류에 따라서 다르게 나타나는 것이라고 볼 수 있지 않을까 한다. 필자는 헤겔의 설명을 이해하기 위해 헤겔의 설명을 다음과 같이 재구성해 보았다.

앞에서 말했듯이 양적 무한성은 정량에 내재하는 운동이며 이는 곧 자기를 부정하는 또는 자기를 넘어가는[Hinaus] 운동이며, 자기를 벗어나는 운동 즉 탈자화[Aussersich]로 규정된다. 그런데 이런 양적 무한성은 정량의 종류에 따라서 다른 방식으로 출현한다. 이를 이해하기 위해 먼저 자연에 존재하는 다양한 운동을 보자. 이 자연의 운동은 수적으로 표현될 수 있다.

등속 운동 S=at a ; 1, 1, 1 (정수): 속도가 고정된 운동

등가속 운동 S=vt v=S/t : 1/2, 2/4, 3/6 (유리수적 분수)…. : 일정한 양으로 속도가 증가하는 운동

가속 운동 S=1/2at² a=2S/t² : 1/2, 1/4, 1/9(무리수적 분수) … : 속도가 가속적으로 증가하는 운동

여기서 세 가지 운동은 전혀 다른 운동으로 보이지만, 사실 하나로 환원될 수 있다. 즉 가속 운동이 단순화된 형태가 등가속운동이고 이 등가속 운동이 단순화된 형태 등속 운동이라는 것이다.

세 가지 운동을 이렇게 본다면, 이 관계를 다시 이렇게 설명할 수도 있다. 양적인 영역에서 운동의 개념은 탈자화하는 운동이다. 즉 자기를 부정해서 또 다른 자기로 이행하는 운동이다. 그런 운동의 개념이 등속 운동에서는 가능성으로만 나타나고 비로소 가속 운동에 이르러 그 개념이 실현된다고 볼 수 있다.

등속 운동에서 운동의 개념이 가능성에 머무르고 감추어져 있다. 무한 진행이 감추어져 있다는 사실은 이 운동에서 운동의 개념인 운동의 기울기가 곧 0라는 것을 통해 표현된다. 그러므로 여기서 운동은 외면적으로만 나타나고 그 결과 운동은 악 무한이나 무한 진행이라는 외적인 모습으로 나타난다.

반면 기울기가 일정수인 경우나 기울기가 증폭하는 경우에서도 그 운동은 무한히 확산한다. 그러므로 여기서도 무한 진행이 나타난다. 그러나 이런 경우에는 운동의 개념이 이미 드러나고 있다. 여기서 운동이 확산하거나 증폭하기 때문이다. 그러므로 그 속에 있는 운동의 기울기가 내적 부정성, 진 무한의 표현이라는 사실을 드러낸다.

자연의 운동이란 본래 두 가지 정량 사이의 관계다. 이는 등가속 운동이나 가속 운동이 분수로 표현된다는 사실을 통해 잘 드러난다. 이런 운동의 개념은 이미 개별 양이 지속적으로 전개되는 등속 운동에서도 감추어져 있다. 그러나 여기서는 드러나지 않을 뿐이다. 따라서 엄밀하게 말하자면 등속 운동도 비례 량이다. 이미 거기서도 두 다른 정량이 관계하고 있다.

등속 운동에서는 비례 량이라는 사실도 드러나지 않기에 여기서는 마치 개별적 정량이 자기 내에서 서로 관계하는 것처럼 보일 뿐이다. 그러나 등가속, 가속 운동에 이르러 운동의 개념이 드러나면서 두 다른 정량의 비례 량이라는 사실이 드러난다.

존재론 현존 절은 판단 형식에서 질적 범주에 해당한다. 존재론 양적인 것은 판단 형식에서 양의 범주를 다룬다. 이때 1절 양적인 것은 양의 운동 일반을 다룬다. 2절 정량은 양의 판단 형식에서 최초의 판단인 단칭 판단의 형식에 해당한다. 그리고 이 단칭 판단이 부정되는 가운데 양적 무한성 개념이 출현하고, 그 결과 등장하는 진 무한은 곧 특칭 판단 형식에 해당한다. 진 무한은 곧 비례 량이니 비례 량이 특칭 즉 양적인 어떤 것에 해당한다.

헤겔 형이상학 산책49-외연량, 내포량, 비례량 [흐린 창가에서-이병창의 문화비평]

2025년 11월 23일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책49-외연량, 내포량, 비례량

앞에서 정량에 두 종류가 있다고 했다. 외연량과 내포량이다. 외연랑은 자기의 한 부분을 단위로 해서 자기를 잴 수 있다. 외연량은 이 단위가 몇 배인가[Vielheit]로 표시된다. 수적으로 표현하자면 외연량은 기수로 표시될 수 있다. 구체적으로는 물체의 길이나 무게와 같은 정량을 예로 들 수 있겠다. 헤겔은 이런 외연량은 “자기 내에서 개수”, “자기 관계하는 다수라는 규정성”을 갖는다고 말한다.

그에 반해 내포량은 이런 몇 배라는 방식으로 표시할 수 없다. 한마디로 여기서는 기본 단위가 발견되지 않는다. 어떤 것의 내포량은 다른 것의 내포량과 비교를 통해 더 많거나 더 적거나 하는 방식으로만[Mehrheit] 표시된다. 수적으로 말하자면 내포량은 다만 서수로만 표시될 수 있다. 예를 들어 다이아몬드가 경도에서 스무 번째라 할 때 그런 점에서 경도가 첫 번째 되는 사물보다 다이아몬드의 경도가 스무 배 더 강하다고 말할 수는 없다. 그저 여러 사물의 경도를 서로 비교해 볼 때 스무 번째라는 말에 지나지 않는다.

내포량은 이처럼 타자와 비교를 통해 나오지만, 여전히 여기서 비교되는 정량은 하나의 정량이며 이는 비교되는 타자와 공유하는 정량일 뿐이다. 즉 물질의 경도나 강도나 감각적 뜨거움이나 가벼움 등과 같은 특정 정량이 비교된다. 그러므로 헤겔은 내포량은 “자기 밖에 있는 것으로서 개수,” “자기에게 외면적인 것으로서 규정성”을 갖는다고 한다.

헤겔은 외연량과 내포량을 넘어서 새로운 정량의 형태로 이행한다. 이 새로운 정량의 형태는 구체적으로 말하자면 비중과 같은 것인데, 이는 두 개의 정량(부피와 무게)의 관계 또는 비례를 통해 형성되는 정량이다. 이제 단순한 정량에서 관계 속에 있는 정량 즉 비례량으로의 이행을 살펴보기로 하자.

자연에는 이처럼 두 개 정량 사이의 관계를 통해 형성되는 정량이 많다. 비중을 예로 들었지만, 비중 외에도 등속도 운동을 보자. 속도는 시간에 비례한다. 등속 운동은 분수로 표현된다. 즉 p=V/t이다. 또 뉴턴의 힘의 법칙에서 힘은 질량이나 가속도에 비례한다.(즉 F=am)

앞에서 수의 종류가 발전하는 가운데 분수가 출현한다고 했다. 분수는 더하기, 곱하기를 거쳐 셈법을 통해 만들어지는 것이지만, 이런 셈법은 단순히 사유의 유희는 아니다. 이런 분수가 곧 두 개의 정량 사이의 관계를 의미한다고 보면, 이 분수는 자연에 존재하는 어떤 정량 즉 두 개의 정량 사이의 관계 또는 비례를 통해 만들어지는 정량을 표현하기 위한 것이다.

이런 분수를 통해 표현되는 정량은 외연량과 내포량보다 더 발전된 정량이다. 외연량이 자기를 단위로 하는 것이라면, 내포량은 타자와 비교하되 결국 동일한 단순한 정량의 측면에서 서로 비교되는 것이다. 그러니 내포량은 자기 관계를 아직 완전히 벗어나지 못한 것이다. 그러나 이제 새로이 등장하는 비중과 같은 비례량은 더는 단순한 정량에 머무르지 않으니, 여기서 비교되는 정량은 비교하는 정량과 전혀 다른 정량이다. 즉 하나의 정량이 타자를 통해 규정되는 것이다. 여기서 비교되는 것은 비교의 대상을 단위로 측정된다.

어떤 것이 단순히 자기 관계하지 않고 타자 관계 속에서 규정된다면, 그것은 질적인 것이 된다. 헤겔에서 질이란 타자의 부정성을 기본 성격으로 가지고 있기 때문이다. 이때 타자는 그 질과 대립하는 타자이며, 이때 두 가지는 반성 관계에 있게 된다. 구체적으로 예를 들자면 헤겔에서 빨강은 항상 빨강이 아닌 색과 대립해서만 빨강으로서 의미를 지닌다.

마찬가지로 하나의 정량이 단순한 자기 관계 속에서 규정되는 것이 아니라 자기와 대립하는 다른 정량을 통해서 규정된다면 그때 이 정량은 질적으로 규정되는 것이라 할 수 있다.

외연량과 내포량은 단순한 정량이다. 그 정량의 한계를 규정하는 방식 즉 몇 배수[Vielheit]냐 아니면 크고작음[Mehrheit]이냐 방식의 차이다. 그런데 외연량과 내포량을 측정할 때 다른 정량과 관계하는 방식으로 측정할 수도 있다. 이렇게 되면 외연량이나 내포량은 서로 환원될 수 있다.

외연적 크기는 내포량을 지닌 정량과 관계하면, 내포적으로 규정된다. 예를 들어 무게를 보자. 무게는 외연량이지만, 만일 피부에 가해지는 압박감을 통해 규정된다면 내포량으로 규정된다. 무거운 것은 강하게 압박하고, 가벼운 것은 약하게 압박한다.

“외연적 크기는 내포적 크기로 이행한다. 왜냐하면, 그 다수의 개수[Vieles]는 그 자체로 그리고 대자적으로 총수 즉 다수의 개수 바깥에 등장하는 총수로 몰락하기 때문이다.”(논리학 재판, GW21, S. 213)

거꾸로 내포량도 외연량을 지닌 다른 정량을 통해서 규정될 수 있다. 예를 들어 감각적 내포량인 뜨거움을 보자. 이 뜨거움은 수은주를 확장하는 효과를 지니는데, 그런 수은주의 확장은 외연량으로 측정된다. 그러므로 뜨거움도 외연량으로 규정될 수 있다.

“다르게 규정된 내포성에 무차별한 것으로서 이 단순한 것은 외면적인 개수를 그 자체에서 가지며, 따라서 내포적 크기는 본질적으로 외연적 크기다.”(논리학 재판, GW21, S. 213)

외연량과 내포량은 사실 단순한 정량이므로 실제 세계에 독립적으로 존재하는 것이라기보다 인간이 필요에 따라 측정하기 위해 추상한 것에 지나지 않는다. 실제 모든 정량은 항상 다른 정량과 관계 속에 있으므로, 이런 관계의 방식에 따라서 외연량은 내포량으로, 내포량은 외연량으로 전환할 수 있다.

거꾸로 말하자면 두 정량의 관계를 통해서 규정된 새로운 정량 즉 비례량은 외연량인 동시에 내포량이라고 할 수 있다. 비례량이라는 개념을 통해 헤겔은 외연량과 내포량을 통일한다. 앞에서 두 정량의 관계 즉 비례량을 통해 양적인 것에서 질적인 것이 출현한다고 했다. 이 두 가지 주장을 연결하면 다음과 같은 헤겔의 말을 이해할 수 있다.

“양자[내포량과 외연량]의 동일성으로부터 질적인 어떤 것이 등장한다. 왜냐하면, 이 동일성은 자기의 구별을 부정하는 것을 통하여 자기에 관계하는 총수이기 때문이다.”(논리학 재판, GW21, S. 213)

정량에는 수의 종류만큼이나 다양한 것이 있다. 수가 분수로 발전하면서 단순한 정량은 관계를 지닌 비례량으로 발전한다.

분수는 다시 두 가지로 구분된다. 유리수에 머무르는 것과 무리수가 되는 것이다. 유리수적 분수가 자연수의 비례 관계로 표현한 것이라면 무리수에서는 제곱의 비례 관계가 출현한다. 예를 들어 등속도 운동 S=vT 와 가속도 운동 S=1/2aT² 을 서로 비교해 보면, 그 차이가 분명하게 드러난다. 만일 분수에서 허수가 개입하게 된다면, 이는 원운동과 같은 것으로 출현할 것이다.

양자는 마찬가지로 분수로 표현되지만, 그 의미는 달라진다. 등속도 운동, 가속도 운동, 원운동은 서로 다른 운동을 표현하는 것으로 볼 수도 있지만, 이들의 관계를 이렇게 볼 수도 있다. 즉 등속도 운동도 하나의 가속도 운동이지만 가속도 운동의 가장 낮은 단계일 뿐이며, 마찬가지로 가속도 운동도 원운동으로 볼 수 있지만, 그 원운동의 가장 낮은 극한에서 등장한 한 운동으로 볼 수 있을 것이다. 이들의 관계를 헤겔적 개념을 가지고 설명한다면, 등속도 운동에서는 개념이 아직 숨어 있고 마침내 원운동에 이르러 비로소 개념이 자기를 실현하는 것으로 볼 수 있다.

마찬가지로 외연량, 내포량, 비례량을 서로 다른 자연의 운동을 표현하는 것으로 볼 수 있다. 그러나 달리 보면, 외연량은 내포량의 가장 낮은 극한이며, 내포량은 비례량의 가장 낮은 극한으로 볼 수 있다. 즉 비례량에서 표면에 드러나게 될 개념이 외연량에서는 감추어져 있다는 것이다.

이제 중요한 것은 이렇게 감추어진 개념을 드러내는 일이다. 그렇다면 이런 숨어 있는 개념이 표면에 드러나는 과정은 어떻게 일어날까? 헤겔은 바로 그것을 부정의 작용으로 본다.

여기서 중요한 것은 부정의 부정이라는 이중 부정인데, 이런 이중 부정을 통해 정량에 감추어진 개념이 드러난다.

이 정량에 감추어진 개념이 곧 무한 개념이다. 헤겔에서 이 무한 개념은 곧 자연의 운동하는 모습을 의미한다. 이어서 헤겔은 2편 2장 3절에서 ‘양적 무한’ 개념을 다루는데, 여기서 헤겔은 비례량에서 드러날 무한 개념을 그 출발점에서부터 추적해 나간다. 무한 개념은 외연량과 내포량, 비례량에서 서로 다른 모습으로 나타난다. 하지만 앞에서 나타난 무한 모습(무한소나 무한대/ 그리고 무한 진행)은 최종적인 비례량에서 나타나는 무한의 모습즉 진 무한을 암시하며 선취하는 것이다. 유의해야 할 것은 무한 개념의 발전 밑에는 정량의 종류에서 발전이 매개되고 있다는 사실이다.

헤겔 형이상학 산책48-셈법과 수의 종류 [흐린 창가에서-이병창의 문화비평]

2025년 11월 23일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책48-셈법과 수의 종류

앞에서 여러 번 수는 정량을 대표하는 정량의 화폐라고 말했다. 이 수를 세는[Zaehlen] 것을 셈법[Rechenschaft]이라 한다. 셈법은 초등학교 들어가서 배우는 제일의 기법이다. 누구나 셈법 하면 더하기 빼기, 곱하기 나누기가 있다는 것을 알 것이다.

더하기 빼기는 그 가운데 더 초보적이고 곱하기에 숙달하려면, 외우는 것이 요구된다. 구구단을 얼마나 외웠는지, 이 나이 들어 자기 전화번호는 종종 기억하지 못하지만, 그래도 구구단은 잘 외운다.

흥미로운 것은 우리는 구구단이라 하는 데 독일 사람들은 일일단[Einmaleins]이라 한다. 이왕 농담하는 김에, 켐브리지 대학교에서 발간한 수학에 관한 소개서에는 이런 말이 나온다. 옛날 그러니까 중세 독일의 한 상인이 자식을 상인으로 키우기 위해 셈법을 가르쳐야 하겠다고 생각했다. 그는 당시 독일 대학교수(아마 수학 교수는 없었고 철학 교수였을 것이다)에게 자식을 데리고 가서 후하게 해 줄 테니 자식에게 셈법을 가르쳐 달라고 했다. 그때 독일 교수가 이렇게 말했다고 한다. “예, 더하기 빼기까지는 저희가 가르칠 수 있지만, 곱하기 나누기를 배우려면, 이탈리아 유학을 가야 합니다.”

이 농담의 전거를 굳이 밝힐 필요는 없을 것이다. 당시 독일에서는 아라비아 숫자를 쓰지 않고, 로마자로 수를 표현했다는 것을 생각하면, 그럴듯하다. 솔직히 지금 필자는 로마자로 된 숫자조차 제대로 읽기 힘들다. 본론으로 돌아가자.

셈법이 이처럼 초등학교에서 배우는 단순한 기술이라고 생각하면 곤란하다. 헤겔이 논리학에서 이 셈법에 관한 철학을 제시했으니 말이다. 좀, 웃길 것 같은데, 사실은 헤겔의 논리학에서 정량에서 무한량 개념으로 이행하는 이유를 이해하는 데서 결정적인 것이다. 이 부분에는 전거를 밝힐 필요가 있겠다.

헤겔 논리학 재판에서 대체로 주석에 관한 한, 초판에서 크게 벗어나지 않는다. 그런데 주석조차 초판을 대폭 확장한 부분이 있는데, 그 부분이 바로 정량과 무한량을 다루는 절에 속한 주석이다. 무한량을 다룬 주석에서는 거의 100쪽에 가까운 광대한 주석을 달아서 소위 해석기하학의 근본원리 즉 무한계산의 원리를 철학적으로 다룬다. 그에 앞서서 정량의 1절(제목 수)에 덧붙인 주석 1에서는 초판의 주석에 덧붙여 바로 이 셈법을 철학적으로 다룬다.

헤겔은 이 셈법에 관하여 다음과 같이 말한다.

“항상 다만 동일한 것을 다루면서도 외면적으로 산출하는 셈법의 상이성은 셈해지는 수들의 상호 차이에 놓여 있다. 그런 구별은 어디 다른 곳에서 외면적인 규정으로부터 받아들여야 한다.”

간단히 말해 셈법의 차이가 곧 수들의 차이에서 나온다는 말이다. 셈이란 동일한 수를 다루는 것이 아닐까? 더하기와 곱하기, 나누기에서 셈하기 전의 수와 셈한 이후의 수는 동일한 수다. 이런 수들은 소위 자연수 가운데 어느 한 위치에 놓여 있는 것이니, 셈법의 차이와 수의 차이는 무관하지 않을까? 그런데도 헤겔은 수의 차이에서 셈법의 차이가 나온다고 하는데, 그 말의 의미는 무엇일까?

셈법에 네 가지가 있다는 것은 다시 말할 필요조차 없을 것이다. 우선 더하기와 빼기를 생각해 보자. 이건 어렵지 않다. 3 더하기 4는, 3개까지 개수를 세고, 더해서 4개의 개수를 더 센 것이다. 이것은 손가락으로 세어보면 쉽게 알 수 있다.

앞에서 말했듯이 여기서 중요한 것은 여전히 개수가 그대로 보존된다는 것이다. 즉 7개의 개수가 아니라 8개나 6개가 되지 않는다. 그러므로 이 명제는 분석적이라 본다. 하지만 이 분석적 명제를 아는 데는 경험적으로 즉 손가락으로 세어보는 것이 필요하다. 왜냐하면, 그 결과가 12개의 개수라는 사실은 분석적으로 알 수 있지만, 그것을 어떤 총수로 표현하는가를 알려면, 손가락의 도움이 필요하기 때문이다.

빼기는 더하기로 환원된다. 3 빼기 2은 3 더하기 -2이다. 즉 3에서 거꾸로 세워가면 된다. 빼기가 더하기로 환원된다고 하더라도, 이미 여기서는 -수가 있다는 사실이 밝혀진다. + 수는 앞으로 가는 것이라면, -수는 거꾸로 가는 것이다. -수가 등장하면서 수가 하나의 벡터 즉 운동하는 방향을 지닌 것이라는 사실이 드러난다. 우리의 시야가 공간의 좌우로 뻗어 나간 것이다.

이제 곱하기를 생각해 보자. 더하기는 1이라는 단위를 개수만큼 반복하는 것이다. 예를 들어 3 곱하기 4에서, 곱하기는 3이라는 총수가 이제 기본 단위가 된다. 그래서 이런 기본 단위를 4번 반복하는 것이다. 즉 3+3+3+3이다. 3은 1+1+1이니, 위의 곱하기는 (1+1+1)+(1+1+1)…로 환원할 수 있어서, 곱하기는 더하기와 다름없는 것으로 보인다.

그러나 수의 기본 계기를 단위, 개수, 총수로 볼 때, 여기서 단위는 총수와 일치한다. 즉 총수가 기본 단위가 된 것이다. 더구나 3 곱하기 4는 4 곱하기 3이나 마찬가지다. 즉 3이라는 총수를 단위로 보고 4를 개수로 보든, 4를 단위로 보고, 3을 개수로 보든, 마찬가지다.

나누기는 곱하기를 변형한 것이다. 3 곱하기 4는 12라는 명제는 12를 4 또는 3으로 나누면 3 또는 4가 된다. 이는 얼마나 여러 번 기본 단위 3이나 4가 주어진 총수 속에 포함돼 있는가를 의미한다. 그 답이 곧 개수다. 또는 나누기는 이렇게도 해석될 수 있다. 즉 어떤 총수를 주어진 개수(3이나 4)에 도달하도록 나누려면 기본 단위를 무엇으로 해야 하는가로 이해할 수도 있다.

어떻든 곱하기와 나누기는 총수를 원하느냐, 개수를 원하느냐, 단위를 원하느냐 하는 요구에 따라 달라지는 표현일 뿐이다. 일정한 과자를 자기 아이들에게 동일하게 나누어주려면 단위가 필요하며, 일정한 과자를 한 아이가 먹을 만큼 나누어주면 몇 명이나 먹일 수 있는가를 생각하려면 개수가 필요하다. 나가서 자기 아이가 먹을 만큼 과자를 사려면 얼마나 사야 하는지, 그 총수를 알려면 곱하기가 필요하다.

더하기는 양수의 영역에서 일어나는 운동이다. 빼기에 이르면 수는 정수로 확장한다. 곱하기는 여전히 정수에 머무르는 것 같지만, 나누기에 이르면 이제 수는 분수의 영역으로 들어가게 된다. 곱하기에는 여전히 자연수에 머무른다. 그러나 그것을 변형한 나누기에 이르면, 자연수를 넘어선 분수가 출현하게 된다.

곱하기는 다시 거듭제곱으로 발전한다. 거듭제곱 예를 들어 3³은 3*3*3이다. 이것은 처음 3이라는 총수가 단위로 되어 3의 개수만큼 반복한다. 그 결과는 9인데 이제 9가 단위가 되어 다시 3의 개수만큼 반복한다. 그러므로 이 거듭제곱은 곱하기로 환원되고, 다시 더하기로 환원될 수 있는 것으로 보인다. 여기서 단순한 곱하기는 반복적이지만 여기서 곱하기는 누적적으로 일어난다. 누적하는 운동이 들어간다.

나아가서 거듭제곱은 새로운 수를 발생한다. 이는 그것에 대립하는 운동인 근의 운동에서 드러난다. 제곱근은 4의 제곱근은 +/-2이어서 지만, 5의 제곱근은 루트로 표현된다. 즉 무리수다. 나가서 삼제곱이나 삼제곱근에 이르면 허수가 등장하게 된다.

이처럼 셈법의 상이한 방식은 수의 종류와 연관된다. 한편으로 셈법이 발전하면서 수의 종류도 발전한 것으로 보인다. 그러나 이것은 우리의 생각이다. 이런 생각은 분수나, 무리수, 허수 등이 인간 사유의 산물로 생각한다. 그러나 헤겔은 오히려 거꾸로 설명한다. 즉 수의 종류는 자연 속에 이미 존재하는 정량의 운동과 관계를 표현하는 것이며, 이 운동과 관계를 우리가 인식 또는 파악하면서 셈법이 나온다는 것이다. 그러기에 헤겔은 앞에서 말했듯이 셈법의 기원은 수의 차이에 있다고 한 것이다.

그렇다면, 수의 종류는 정량의 어떤 관계를 표현하는 것일까? 헤겔은 두 가지를 집중적으로 설명하는데, 분수와 무리수다. 무리수는 나중에 무한량(미분양)과 관계되는 데, 우선 정량을 다루는 데서는 분수가 중요한 의미를 지니고 있다.

우선 분수를 보자. 그런데 분수란 무엇인가? 헤겔은 이 분수를 단순한 수의 관계가 아니라 자연에 존재하는 두 가지 정량의 관계를 표현하는 것으로 본다. 예를 들어 비중은 질량과 부피의 관계다. 가속도는 힘과 질량의 관계다. 분수는 이런 두 개의 정량이 갖는 관계를 표현하기 위해 고안된 것이다.

자연 속에 정량은 하나의 양이다. 이 정량은 동일한 일자의 반복적 관계이며, 이 정량은 외연량과 내포량으로 구분된다. 앞에서 설명했듯이 외연량은 자기의 한 부분으로 자기를 측정한다. 이는 단순한 자기 관계다. 헤겔에서 단순하다는 것은 추상적이라는 말이며, 개별적이라는 의미다. 예를 들어 길이나, 무게 등등 각각은 이런 추상적인 개별적 정량이다.

그런데 내포량에 이르면 이 내포량은 이런 추상적인 단순한 자기 관계를 벗어난다. 내포량은 다른 것과 비교해서만 측정되며, 즉 어떤 것은 다른 것보다 어떤 점에서 더 많고 더 강한 것이다. 헤겔은 이런 내포량은 타자를 매개로 해서 자기 관계하는 정량이라고 규정한다.

내포량에서는 아직 하나의 정량이 다른 정량에 대한 관계가 출현한 것은 아니다. 다른 것과 비교되지만, 그러나 비교되는 것 자체는 동일하다. 즉 다이어몬드의 강도와 유리의 강도가 강도라는 하나의 정량에서 비교된다.

그러나 이제 내포량을 넘어서 하나의 정량이 다른 정량과 관계하는 것을 통해서 출현하는 정량이 등장한다. 그게 바로 앞에서 예로 든 비중이나 가속도와 같은 것인데, 수로 보면 이런 관계는 분수 즉 비례나 관계로 표현된다.

그러므로 수가 분수가 된다는 것은 사유의 유희가 아니라, 자연 속에 존재하는 두 정량의 관계를 표현하기 위해 분수가 고안된 것이다. 헤겔은 정량이 다른 정량과 관계하면 이 관계를 통해 질적인 정량이 등장한다고 본다. 양에서 다시 질이 되돌아온 것이다. 비중이나 가속도는 양적인 것이지만, 이미 질적인 성격을 지닌 것이다.

앞에서 질을 설명하면서 두 성질의 상호 관계를 통해서 대자 존재가 출현하고, 이로부터 양적인 것이 출현했다고 했다. 이제 거꾸로 양이 서로 관계 맺으면서 질을 발전시킨다. 이 질은 단순한 감각적 성질이 아니라 질적 성격을 지닌 양적인 것이라는 것이다. 양이 질로 발전한다는 사실은 양적인 것과 질적인 것을 대립하는 것으로 보고, 심지어 양적인 것을 자연에서 제거하려는 철학자들에게는 충격적인 주장이 될 것이다.

헤겔 형이상학 산책 47-수학적 명제는 선천적 종합 명제인가? [흐린 창가에서-이병창의 문화비평]

2025년 11월 15일/0 Comments/in 문화 & 생각보기, 흐린 창가에서-이병창의 문화 비평 /by 병창 이

헤겔 형이상학 산책47- 수학적 명제는 선천적 종합 명제인가?

논리학은 정량을 다루는 가운데, 수 개념을 제시한다. 이 수는 정량을 대표하는 것 즉 상품을 대표하는 화폐와 같은 것이다. 그러므로 수가 지닌 모든 속성은 정량에서부터 유래한다.

이런 관점에서 헤겔은 수학에 관한 여러 가지 철학적 논의에 개입하는데, 그 가운데 하나가 바로 칸트가 <순수 이성 비판>에서 제시한 주장 즉 ‘수학적 명제는 선천적 종합 명제다’라는 주장이다. 헤겔은 이를 주석에서 다루는데, 그의 주장에는 우리의 흥미를 끌 만한 요소가 있어 여기 소개한다.

알다시피 칸트는 아주 기초적인 수학적 명제를 예로 든다. 즉 ‘7+5는 12라는 명제’다. 칸트는 여기서 ‘더하기’라는 개념을 분석하더라도, 그 더해진 수가 ‘12’라는 사실은 나오지 않는다고 한다. 이 12라는 수를 발견하기 위해서는 우리는 손가락을 이용해 7개를 세고, 더 나가서 5개를 더 세어야 한다. 이렇게 세어진 결과 구부려진 손가락을 직관하면서, ‘12’라는 수를 떠올린다. 그러므로 칸트는 개념을 넘어서 경험적 직관의 도움 없이는 위의 명제를 알 수 있는 길이 없다고 말한다.

헤겔은 칸트의 이런 주장을 비판하면서, 위의 수학적 명제는 분석적 명제라고 말한다. 즉 경험적 직관의 도움이 없어도 위의 명제가 진리라는 것을 알 수 있다는 것이다. 왜냐하면, 수에서 ‘더하기’란 가장 외면적인 관계를 말하기 때문이다.

앞에서 양적인 것은 대자 존재적인 일자들 사이에 서로 외면적인 관계, 서로 동등하면서도 서로 구분되는 관계를 다룬다고 했다. 양자의 서로 동등한 관계가 곧 물질적 관계며, 양자의 서로 구분되는 관계가 공간적 관계다. 물질적인 관계와 공간적 관계는 상호 동전의 양면이다.

이런 양적인 것의 관계는 가장 외면적인 관계다. 여기서 서로 관계하는 일자들 사이에 어떤 내적인 연관도 존재하지 않기 때문이다. 이런 외면성은 기하학적 공간을 생각해 보면 충분히 이해할 수 있을 것이다. 기하학적 공간은(일단 여기서는 유크리트적 공간을 말한다) 텅 비고 동질적이어서 그 속에서 도형을 아무리 이리저리 이동하더라도 그 도형은 서로 합동이며 즉 도형의 내적 성질은 그런 공간적 이동에 전혀 영향을 받지 않는다. 마찬가지로 양적인 것은 가장 외면적 공간이어서 그 속에서 정량들이 맺는 관계는 그 정량들에 아무런 영향을 미치지 못한다.

그러므로 7개에 5개를 더하더라도, 전자의 개수가 7개인 것에는 변함이 없고 후자에 개수 5개 역시 그대로 남아 있으니, 12개의 개수가 보존된다는 사실은 분명하다. 중요한 것은 12개의 개수가 보존된다는 것이다. 이는 어떤 직관이나 경험의 도움이 없이도 알 수 있는 사실이며 이는 분석적인 사실이다.

칸트는 12개의 개수가 있을 때 이를 ‘12’라는 총수로 표현하기 위해서 경험의 도움을 받아야 한다고 했으나, 이것은 언어적 표현의 문제이다. 12개의 개수를 ‘12’라는 수로 표현하는 것은 12라는 수의 의미를 이해하는 사람이라면 누구나 그런 언어로 표현할 것이다. 만일 12개의 개수를 표현하는 언어가 ‘12’라는 수가 아니라, ‘한 다스’라는 언어이어서 그 결과를 ‘한 다스’로 표현하더라도 문제는 없다. 어떤 언어로 표현하느냐는 언어적 문제이지 ‘더하기’라는 사태의 본질은 아니다.

칸트가 수학이 선천적 종합 명제라는 주장의 예로 또 하나 끌어들인 것이 기하학의 명제다. 그것은 곧 ‘직선은 두 점 사이의 최단 거리다’라는 명제다. 이 명제가 선천적 종합 명제라는 주장에 대한 칸트의 논증은 간단하다. 직선이라는 개념은 질적인 개념이다. 직선은 ‘곧바른’, ‘단순한’ 선이라는 말이니 말이다. 반면 ‘최단은 양적인 개념이다. 즉 길이가 가장 짧은 것이라는 의미다. 질적인 개념에서 양적인 개념이 나오지 않으니, 위의 명제는 분석적인 것으로 이해할 수 없다. 이는 경험을 통해서만 알 수 있는 명제다.

헤겔은 여기서 칸트가 직선 개념을 오해했다고 한다. 직선은 단순히 성질을 의미하는 것이 아니다. 오히려 직선에는 이미 양적인 개념이 들어 있다. 즉 직선은 그저 ‘곧바른 것[Gerade]’ 가 아니라 ’곧바른 선[Gerade Linie]’이므로 위의 기하학적 명제는 양적인 개념에서 양적인 개념을 끌어낸 것일 뿐이다.

이렇게 칸트를 반박한 다음, 헤겔은 직선 개념에서 최단 개념을 아래와 같은 방식으로 끌어낸다. 직선은 가장 ‘단순한’ 선이니 ‘자기 관계하는’ 선이고, 이런 ‘자기 관계’는 “어떤 종류이든 규정의 상이성이나 그 바깥의 점이나 선에 대한 관계도 정립되지 않은 것”이니, 따라서 ‘최단’의 선이다는 것이다. 그 논증의 핵심은 곧 직선은 두 점 사이에 놓인 축에서 벗어난 제3의 점을 거치지 않으므로, 즉 우회를 거치지 않으므로 최단일 수밖에 없다는 생각에 기초한다.

“직선이라는 규정은 사실 다름 아니라 단적으로 단순한 선이다는 즉 그 탈자화(점의 운동) 가운데 단적으로 자기 관계하며, 그 확장 속에서 어떤 종류의 상이한 규정이나 자기 바깥의 점이나 선에 대한 어떤 관계도 성립하지 않는, 단적으로 자체 내 단순한 벡터[Richtung]라는 의미다.”(논리학 재판, GW21, S. 200)

헤겔의 논증은 겉으로 보기에도 좀 억지 또는 궤변처럼 보인다. 기하학적 명제에 관한 한, 칸트가 말한 것처럼 경험적 성격이 있다는 사실을 인정할 수밖에 없을 것 같다. 비유클리드 기하학이 등장하면서 기하학적 논증이 일정한 특수한 공간에서 성립한다는 사실이 밝혀졌기 때문이다.

<정신현상학> 서문에 보면, 거기서 헤겔은 기하학적 명제의 증명이 작도에 의존하며, 그런 작도는 경험을 통해 우연히 발견된 것이라는 사실을 들어서, 기하학적 명제가 순수하게 개념적이며 분석적이 아니라고 주장한다. 그러므로 헤겔은 여기서 비록 칸트가 예로 들기는 했더라도, 굳이 기하학적 명제를 끌어들여, 수학이 분석적이라는 자신의 주장을 혼란스럽게 만들 필요가 없었을 것이다.

다행히 기하학은 해석기하학을 통해 수학으로 환원됐으며 해석기하학은 특수한 공간에 적용되는 유클리드 기하학과 달리 순수한 양적인 공간 속에서 전개되는 것이다. 그러므로 수학적 명제의 성격에 관해서 이미 다분히 경험적인 기하학적 명제를 끌어들이지 않고 수의 관계를 통해서 분석하는 것으로 충분할 것이다.

알다시피 칸트는 이런 수학적 명제는 경험적이면서도 필연적(보편적)이어서, 그 때문에 선천적 종합 명제라 불렀다. 흥미로운 것은 헤겔이 앞에서 말한 것처럼 수학적 명제가 경험적이라는 사실을 부정한 것에 그치지 않고 나아가서 수학적 명제가 필연적이라는 사실 역시 부정한다는 것이다.

그런데 헤겔은 수학적 명제가 분석적이라고 했다. 분석적이라면 필연적이 아닌가? 적어도 칸트의 용법에서는 그렇다. 그런데도 헤겔은 그 필연성을 부정하는데, 그 이유가 무엇인가?

여기서 헤겔의 필연성 개념의 의미를 이해해야 한다. 헤겔에서 필연성은 사태가 내적으로 연관돼서. 연관된 하나의 사태에서 다른 사태로 이행하는 것이 필요하고도 충분한 경우를 말한다. 그런데 수학적 명제가 토대를 두고 있는 양적인 것의 관계는 서로 외면적인 것이다. 동일한 일자가 반복되면서 맺는 양적인 관계는 같은 것의 반복(물질적 측면)이어서 연속적이며 그런 한에서는 전적으로 동어반복적인 필연성을 지닌다. 그러나 동시에 이 관계는 서로 단적으로 다른 것의 관계(공간적 측면)이어서 불연속적이며 그런 한에서는 서로 무차별하다. 이런 무차별한 측면에서는 그 관계는 전적으로 우연적인 것이다.

다시 말해 수의 관계를 보면, 같은 것의 반복이라는 측면에서 분석적이다. 그러나 다른 것의 관계라는 측면에서 전적으로 우연적인 것이다. 다시 말하자면, 구체적 사물을 일자라는 것으로 추상화해서, 즉 단순한 물질이나 공간으로 볼 때, 이 사물의 수적 관계는 분석적이다. 그러나 어떤 일자를 구체적인 것으로 본다면, 이것들의 관계는 비록 수학적으로 표현되더라도 필연적이 아니고 우연적이다.

즉 손가락을 추상화하며 동일한 일자로서 볼 때 여기서 더하기는 분석적이다. 그러나 손가락을 구체적 사물로 볼 때(수자는 본래 손가락을 지시하는 명사였다는 것을 기억하라), 즉 손가락 두 개로 보지 않고 예를 들어 엄지와 검지, 중지로 보면, 이런 구체적 사물의 관계에서 더하기라는 관계 자체가 성립하지 않는다. 엄지와 검지를 더한다는 것은 무의미하며, 이를 통해 중지가 나온다는 것도 불가능하다. 이런 관계는 그때그때 구체적인 관계이며, 수적인 필연성을 지닌 관계는 아니다.

여기서 흥미로운 생각이 떠오른다. 칸트는 수학적 명제를 선천적 종합 명제라 했다. 헤겔은 수학적 명제는 분석적 우연의 명제로 보아야 한다고 한다. 최근 언어철학자 크립케는 고정지시어를 경험적이며 필연적 명제라 했는데, 그의 주장은 칸트에 가깝다기 보다 헤겔에 더 가깝다.

수학적 명제가 이처럼 추상적인 일자의 관계 즉 추상적인 물질이나 공간에서나 적용되는 것이라는 측면에서 헤겔은 수학의 한계를 본다. 근대에 들어와 수학은 자연과학의 도구로서 혁혁한 성과를 거두었다. 그 때문에 철학자들은 수학적 관계를 일반화해서 세계의 모든 관계를 표현하려 시도했다. 즉 수학을 철학의 방법으로 끌어들인 것이다. 헤겔은 자연과학에서 수학이 놓아준 성과를 무시하는 것은 아니다. 헤겔은 역학적 물체를 다루는 영역은 전적으로 양적인 영역이니, 여기서 수학을 적용하는 것은 당연하고 필요한 일이라 한다. 수는 정량을 대표하는 것이기 때문이다.

헤겔은 이를 충분히 인정하는 가운데서도 수학적 관계를 일반화해서 자연 전체를 즉 생물학이나 심지어 인간 사회를 이해하는 도구로 사용하려 할 때 이런 철학적 시도에 관해서는 비판적이다. 생물이나 인간의 경우에는 이미 더 복잡한 물질적 체계를 가지고 있으니, 여기에 수학적 관계를 적용한다는 것은 생물이나 인간을 역학적 물체로 환원하는 것에 해당하기 때문이다.

“구체적인 진정한 사상, 가장 생동적이며 가장 운동적이고 단지 관계 속에서만 개념화되는 것이 이같은 탈자의 지반[즉 수] 속으로 옮겨지면서 죽은 운동이 없는 규정으로 변한다. 따라서 사상의 규정과 관계가 풍부할수록 수와 같은 형식으로 사상을 표현하는 것은 더욱 황량하고 자의적인 것이 된다.”(논리학 재판, GW21, S. 205-6)

물론, 헤겔은 수학적인 것이 감각적인 것과 사상의 가운데 있는 추상적인 일자의 영역 즉 양적인 영역이므로 수학적인 것은 사유를 통해 사상에 다가가는 예비적 단계로서 사유를 훈련하는 데 도움이 된다고 본다. 그런 점에서 철학자가 수학을 배우는 것은 마땅한 일이라고 본다.

그리고 사상을 상징하는 하나의 기호로 수를 사용한다는 것도 도움이 된다고 본다. 기호이란 표면적인 유사성(도상)이나 단편적 흔적(지표), 관습적 관계(상징)만으로도 상징으로서 충분한 역할을 다할 수 있기 때문이다. 예를 들자면 삼위일체와 같은 수학적 상징이 그러하다.

그러나 헤겔은 ‘삼위일체’라는 수학적 상징은 개념의 발전 즉 일반성, 특수성, 개별성 사이의 내적 필연적 연관을 성자, 성부, 성령과 같은 자연적인 가족적 관계로 오해하게 만들었다고 한다. 이처럼 이런 수학적 상징은 수가 서로 무차별하게 존재하는 것이므로 개념의 내적 발전이나 연관을 은폐함으로써 오히려 그 진정한 의미를 이해하는 것을 어렵게 하기도 한다는 한계가 있다. 다음과 같은 헤겔의 한탄을 들어보라.

“고대인은 사상규정을 위한 수적 형식의 불충분성을 매우 올바르게 통찰하고 있었으며 사상을 위한 임시변통 대신에 사상에 본래적인 표현을 마찬가지로 올바르게 요구했다. 고대인들은 숙고의 측면에서 오늘날 사람들보다 얼마나 더 나았는가, 왜냐하면, 오늘날 사람들은 다시 수 자체와 수적 규정을 … 사상 규정 대신에 정립하면서 무능력한 유아 단계로 되돌아가는 것을 어떤 가상할 만한 것이며 근본적이며 심원한 것으로 여긴다.”(논리학 재판, GW21, S. 205)