플라톤의 <국가> 강해(67) [이정호 교수와 함께하는 플라톤의 『국가』]

플라톤의 <국가> 강해(67)

C. 철인 통치자의 교육 목표와 교과목(502c-541b)

3.선분의 비유(509c-513c) – (I)

[509c-513c]

* 소크라테스가 좋음의 이데아가 갖는 특별한 지위에 대해 설명하자 글라우콘은 신령스러운 넘어섬이라고 놀라워 한 후 그것이 갖고 있는 태양과의 유사성과 관련하여 조금도 빠짐없이 설명해달라고 요구한다.(509c)

* 이에 소크라테스는 남겨 놓은 이야기가 많고 또 많은 것을 빠뜨리게 될 테지만 그래도 최대한 이야기하겠다고 말한 후 다시 한 번 가지적인νοητός 영역τόπος과 가시적인ὁρατός 영역을 구분한 후 그 두 영역에 있는 두 가지 부류γένος들을 크기가 다른 ‘두 부분으로 나뉜’δίχα τετμημένην 선분γραμμή에 비유하여 아래와 같이 설명하기 시작한다.(509d)

1) 크기가 다른ἄνισα 두 부분τμῆμα으로 나뉜 선분을 다시 동일한 비율로 ‘가시적인 종류의 부분’τό τοῦ ὁρωμένου γένος과 ‘사유되는 종류의 부분’τὸ τοῦ νοουμένου γένος으로 나눈다.

2) 이것들을 서로 간의 상대적인 명확성σαφήνεια과 불명확성ἀσαφείᾳ의 관점에서 보면 가시적인 종류의 한 부분은 모상εἰκών들이다.(509e) 이 모상들은 그림자σκιά들, ‘물에 비친 영상들’τὰ ἐν τοῖς ὕδασι φαντάσματα, 밝고 조밀하고 매끄럽게 만들어진 것들에 비친 영상들 그런 모든 것들이다. 가시적인 종류의 다른 한 부분은 이 모상들이 닮아있는 원본들, 즉 우리 주위의 동물들 τά περὶ ἡμᾶς ζῷς과 모든 식물들 τὸ φυτευτὸν, 그리고 인공물τὸ σκευαστὸν의 종류 전체이다.(510a)

3) ‘진리와 진리 아님’ἀληθείᾳ τε καὶ μή의 관점에서 보면 위와 같은 가시적인 부분은 믿음(의견)의 대상τὸ δοξαστὸν이 앎의 대상τὸ γνωστόν과 맺고 있는 관계와 마찬가지로, 닮은 것τὸ ὁμοιωθὲν이 그것이 닮아있는 원본τὸ ᾧ ὡμοιώθη과 맺게 되도록 나뉘었다.(510a)

4) 그리고 가지적인 것의 부분의 경우, 한쪽은 앞에서 모방되었던μιμηθεῖσιν 것들을 모상εἰκών으로 사용하면서 영혼이 가정ὑπόθεσις으로부터 출발해서 첫 원리ἀρχή가 아니라 결론τελευτή을 향해 진행하며 탐구ζητεῖν할 수밖에 없는 부분이고, 다른 쪽은 가정으로부터 출발해서 ‘가정이 놓이지 않은 첫 원리’(무가정의 원리)를 향해 나아가며 저쪽에서 사용한 모상들 없이 형상εἶδος들 자체αὐτός만을 사용해서 그것들을 통해 탐구μέθοδος를 해나가는 부분이다.(510b)

* 소크라테스가 가지적인 것의 부분들을 ‘가정’이란 말을 끌어들여 설명하자 글라우콘은 충분히 이해하지 못했다고 말한다. 이에 소크라테스는 그것을 아래와 같이 설명한다.

1) 기하학γεωμετρία이나 계산술λογισμός이나 그러한 것들을 하는 사람들의 경우, 홀수τό περιττὸν와 짝수τὸ ἄρτιον, 도형들τὰ σχήματα과 세 종류εἶδος의 각γωνία 그리고 그것들과 유사한 다른 어떤 것들을 가정으로 놓고서는 마치 이런 것들을 아는εἰδότες 사람들인 양, 그에 대한 어떤 설명λόγος도 제시할 필요가 없는 것, 모두에게 분명한 것으로 여긴다.(510c)

2) 그리고 이것들로부터 시작해서 나머지 것들을 검토해가면서 일관성이 유지되는 방식으로ὁμολογουμένως 그들이 애초에 고찰하고자 했던 것에까지 도달한다.(510d)

3) 기하학자, 계산술 그러한 것들을 하는 사람들은 눈에 보이는ὁρωμένος 도형εἶδος들을 사용하며 이것들에 대해 논의를 하지만, 그들이 사고하는διανοούμενοι 대상은 이것들이 아니라 ‘이것들이 닮아있는 그 원본들’οἷς ταῦτα ἔοικε이다. 그들은 자신들이 그리는 사각형τετράγωνος이나 대각선διάμετρος이 아니라 ‘사각형 자체’나 ‘대각선 자체’αὐτῆς를 ‘염두에 두고’ποιοῦνται 논의를 하는 것이다.(510d-e)

4) 그리고 그들은 자신들이 만들고 그린 바로 그것들을(그것들의 경우 그것들의 그림자σκιά나 물ὕδωρ에 비친 모상εἰκών들도 있다) 이번에는 모상으로 사용하는데(510e) 그렇게 하는 까닭은 사고διανοίᾳ를 통해서만 볼 수 있는ἰδεῖν 저것들 자체αὐτὰ ἐκεῖνα(사각형 자체나 대각선 자체)를 보기 위해서이다.(510e)

5) 이것들은 가지적인 부류에 속하는 것이지만 이것의 탐구ζήτησις에서 영혼은 가정을 사용하도록 강제되고ἀναγκαζομένην 가정들보다 더 위로 넘어갈ἀνωτέρω ἐκβαίνειν 능력이 없어서 ‘첫 원리’ἀρχή로 나아가지는 못한다.(511a) 그리고 그 아래의 것들에 의해 모방되며 그 아래의 것들에 비해서는 분명한ἐναργής 것이라고 판단되고δεδοξασμένοις 존중받는τετιμημένοις 것들, 바로 그것들을 그들은 모상εἰκών으로 사용한다. 이런 것들이 기하학γεωμετρία이나 그와 유사한ἀδελφή 전문기술들τέχναι에서 일어나는 일이다.(511a)

* 소크라테스는 가지적인 부류에서 기하학이나 계산술과 같이 가정을 사용하는 경우를 위와 같이 언급한 후에 가지적인 것의 다른 한쪽 부분으로 가정을 전혀 사용하지 않는 경우를 아래와 같이 언급한다.

1) 이러한 경우란 이성 자체αὐτὸς ὁ λόγος가 ‘변증술적 대화(문답)의 능력을 통해’τῇ τοῦ διαλέγεσθαι δυνάμει 파악하는 경우로서 여기에서 이성은 가정들을 ‘첫 원리’가 아니라 말 그대로 가정들로 삼아 그 가정들을 가정이 놓이지 않은ἀνυποθέτου(무가정의) 것, 즉 ‘모든 것의 첫 원리’τοῦ παντὸς ἀρχὴ에 이를 때까지 거기를 향해 나아가기 위한 출발점ὁρμή이자 디딤 발판ἐπίβασις 같은 것으로 삼는다.(511b) 그리고 그렇게 첫 원리를 파악하고 나면 이성은 다시 거꾸로 첫 원리에 근거를 둔 것들에 의존하면서 결론까지 그런 식으로 내려간다.καταβαίνῃ.(511b)

2) 이러한 파악 방식은 감각될 수 있는 것αἰσθητῷ은 어떤 것도 전혀 사용하지 않고 ‘형상들 자체를 사용해서 형상들을 통해 형상들로 나아가 형상들로 끝을 맺는 방식이다.εἴδεσιν αὐτοῖς δι᾽ αὐτῶν εἰς αὐτά, καὶ τελευτᾷ εἰς εἴδη”(511b)

* 소크라테스의 이와 같은 설명에 글라우콘은 엄청난συχνός 일ἔργον을 말씀하고 계시는 것 같다고 말한 후 그 내용을 아래와 같이 자기 나름으로 정리한다.

1) 전문기술이 고찰하는 부분보다 ‘변증술적 대화를 할 줄 아는 앎’τὸ ὑπὸ τῆς τοῦ διαλέγεσθαι ἐπιστήμης이 고찰하는θεωρούμενον ‘있는 것’το ὄντος과 ‘가지적인 것’το νοητος의 부분이 ‘더 명확한 것’σαφέστερον이라고 규정διορίζειν할 수 있다.(511c)

2) 전문기술들에서는 가정들이 첫 원리들이며, 자신들이 구경하는 것들을 감각이 아니라 사고를 통해서 구경하도록θεᾶσθαι 강제되지만, 첫 원리를 향해 올라가지ἀνελθόντες 않고 가정들로부터 그것들을 살펴보기σκοπεῖν 때문에 이들이 그것들에 관해 지성νοῦς을 가지고 있지는 않다(511c-d)

3) 기하학자나 그런 사람들의 상태는 지성이 아니라 사고διάνοια라고 부르는 것 같다. 사고dianoia는 믿음δόξα과 지성의 중간μεταξύ에 있는 어떤 것이기 때문이다.(511d)

*소크라테스는 글라우콘이 자신의 설명을 아주 충분히 잘 받아들였다고 평가한 후, 위에서 설명한 네 부분τμῆμα에 상응해서 아래와 같이 네 가지 영혼의 상태παθήματα가 생긴다고 말한다. 요컨대 맨 윗부분에 ‘지성적 앎’νόησις이 두 번째 부분에 사고διάνοια가, 세 번째 부분에는 확신πίστις이, 마지막 부분에 짐작εἰκασία이 할당된다. 이것들이 대상으로 하는 것들은 그것들이 진리 ἀληθεία에 참여하는μετέχει 만큼 명확성σαφήνεια에 참여하며 그것들은 그 비율에 따라ἀνὰ λόγον 배열을 이룬다.(511d-e)

——————————-

* 509d-e ‘크기가 다른 두 부분으로 … 동일한 비율로 나누게’ : ‘크기가 다른(anisa)’으로 읽어야 하는지 ‘크기가 같은(an isa)’으로 읽어야 하는지 논란이 있지만 대부분 경우 ‘크기가 다른’으로 읽는다. 이에 따라 구분된 선분을 도표화하면 아래와 같다.

    L1          L2          L3               L4

l——–l—————l—————l————————-l

L1과 L2 = 가시적인 종류의 것

L1 = 모상들(그림자, 영상) L2 = 실물들(식물, 동물, 인공물)

L3와 L4 = 가지적인 종류의 것

L3 = 가정들(수, 도형, 각)을 놓고 가는 것, L4 = 무가정적인 것, 첫 원리, 형상들-

명확성과 불명확성에 따른 각 선의 길이 비율

L1 : L2 = L3 : L4 = L1+L2 : L3+L4

* 각 선의 비율은 명확성에 있어 가시적인 것에 대한 가지적인 것의 우위와

각 영역 내에서 L1에 대한 L2의 우위, L3에 대한 L4의 우위를 나타내기 위한 것이다.

전체적으로는 L1보다는 L2가, L2보다는 L3가, L3보다는 L4가 명확성에서 우위에

있음을 보여주기 위한 것으로 판단된다. 그러나 실제 크기를 보면 L2와 L3가 같다.

혹자는 이것을 근거로 둘 간의 명확성의 크기가 같다고 주장하나 그것이 같음에 대한 언급이 전혀 없다는 점과 표를 통해 드러내려는 플라톤의 기본 의도를 고려하면 도표상 그것들이 결과적으로 같은 길이로 나타날지를 플라톤 자신 미처 몰랐을 수가 있다.

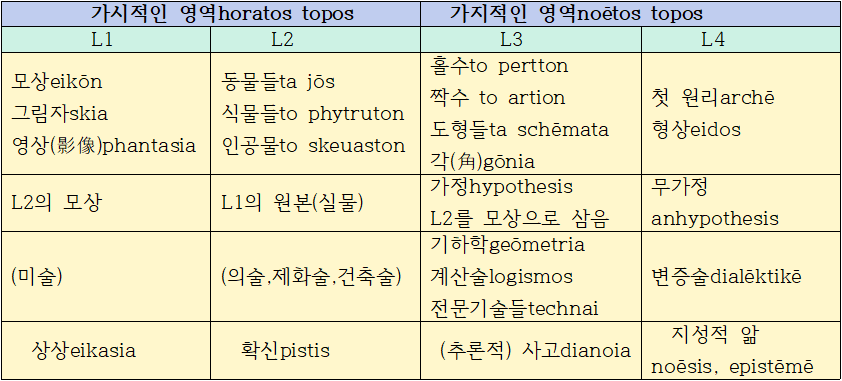
* 플라톤이 위에서 말하고 있는 선분의 비유의 내용을 도표로 나타내면 다음과 같다.

* ‘믿음’은 그리스어 doxa의 역어이다. 그런데 이번 강해에서는 ‘믿음’이라는 역어가 선분의 비유에 나오는 ‘확신pistis’이란 역어와 혼동될 수도 있다는 점에서 ‘믿음’에 ‘의견’이란 말을 병기했다. 플라톤에게 pistis는 doxa에 포함된 것이되 신뢰성에서 상상보다는 높은 사고보다는 낮은 수준의 생각과 견해를 말한다.

* L3의 대상이 홀수, 짝수, 도형들, 각으로 예시되면서 아리스토텔레스는 L3의 대상을 ‘수학적인 것들’ta mathēmatika로 부르고 있다.(<형이상학> A.987b15) 플라톤은 그것을 구체적으로 ‘기하학이나 이와 유사한 학술들’(511b) 즉 수학, 평면 기하학, 입체기하학, 천문학, 화성학이 다루는 대상들로 표현하고 있다.

* ‘사고’dianoia는 사전적 의미에서 뭔가를 목적으로 하는 지적인 궁리이되 논리적 추론이나 설명을 기반으로 하는 개념적 사고를 말한다. 선분의 비유에서 그 말은 기하학 등 전문 학술들의 인식 단계를 나타내는 말로 쓰인다.

* 511b ‘내려간다.’katabainē’ : 이성이 첫 원리를 파악한 후 다시 거꾸로 사고 단계로 내려갈 때 사용되고 있는 동사 ‘내려간다.’katabainō는 동굴의 비유에서 이데아를 본 사람이 다시 동굴로 내려갈 때도(516e) 쓰이고 <국가> 첫 구절 ‘어제 나는 아리스톤의 아들 글라우콘과 함께 페이라이에우스로 내려갔다’(327a)에도 나온다. 그래서 어떤 사람들은 본문 첫 강해 때도 언급했듯이 <국가> 첫 구절에 모종의 상징성을 부여하여 그 말과 연계지어 그 말들이 ‘현상의 구제’를 함축하는 말로 다소 과도하게 의미 부여하기도 한다.

* 511c에서는 ‘본다’를 의미하는 동사가 두 군데 나온다. 하나는 ‘변증술적 문답을 할 줄 아는 앎이 고찰하는 있는’이란 구절에서 ‘고찰하는’으로 번역된 ‘theōroumenon’(원형 theōreō)이고, 또 하나는 ‘전문기술들에서는 사고를 통해서 구경하도록 강제되지만’이란 구절에서 ‘구경하도록’으로 번역된 ‘theasthai’(원형 theaomai)이다. 둘 다 기본적으로 ‘본다’(look at, see)라는 뜻을 갖고 있지만 전자는 ‘관조’theōria의 의미가 그러하듯 의미상 speculate, consider 등 지성적 함축을 많이 포함하고 있고, 후자는 오늘날 극장theatre의 어원 theatron에서 thea가 의미하듯 ‘관망’view as spectators의 의미가 크다. 플라톤은 여기서 앎과 사고의 차이에 준해 그 표현들을 구분해서 사용하고 있다. 그리고 476a에서 ‘앎을 좋아하는 철학자들’과 대비하여 ‘전문 기술을 좋아하는 사람들’philotechnos을 ‘구경을 좋아하는 사람들’philotheamōn로 일컫고 있는데 이 때 theamōn도 theaomai에서 나온 말이다. 여기서 theaomai를 ‘구경하다’로 번역한 것도 그 때문이다. 플라톤은 일상어의 이러한 미묘한 차이까지 의식하면서 생각을 표현하고 있다. 사소할지 모르지만 최소한 플라톤철학 연구자라면 텍스트상의 이러한 차이를 간과해서는 안 된다.

——————————-

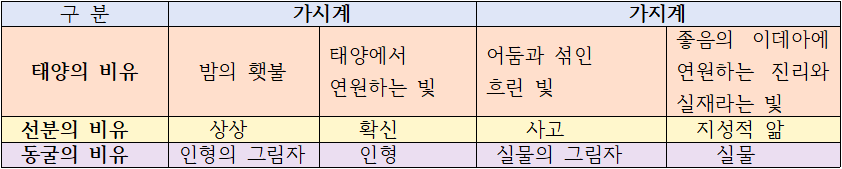
* 선분의 비유와 동굴의 비유는 ‘좋음의 이데아와 태양과의 유사성만은 빠짐없이 다시 자세히 설명해 달라’는 글라우콘의 요구(509c)에 따라 제시된 비유들이다. 즉 우리가 지금 다루게 될 선분의 비유와 이어지는 동굴의 비유는 모두 태양의 비유와의 유사성에 착안하여 좋음의 이데아에 대한 추가적인 설명의 일환으로 제시된 것이다. 그래서인지 선분의 비유는 태양의 비유와 마찬가지로 전체 구도상 가시적인 영역과 가지적인 영역을 구분하는 방식으로 시작되고 마지막 동굴의 비유 또한 동굴과 바깥세계, 어둠 속 횃불과 대낮의 대비 형식으로 내용상 비슷한 구도로 전개되고 있다. 게다가 그 두 영역 모두 다시 각기 마치 명백성의 단계를 보여주듯 크게 두 부분으로 나누어져 있어 학자들은 그 모든 비유가 아래와 같이 대체로 비슷하게 전체적으로 4단계로 구분되어 있다고 여긴다.

* 좋음의 이데아는 <국가>는 물론 플라톤 철학 전체를 이해하는데 중대한 관건이 되는 핵심 주제이다. 그럼에도 그것을 이해하기 위해 <국가>에서 우리가 들여다볼 수 있는 직접적인 전거는 위의 세 가지 비유들밖에 없다고 해도 과언이 아니다. 그래서 많은 학자들은 그 세 비유의 의미를 이해하기 위해서 그 세 비유 간의 상호 관계 특히 각 비유가 포함하고 있는 단계별 영역 간 유사성과 상응 관계를 구체적으로 비교 분석하고 그것을 통해 플라톤이 말하고자 하는 근본 의도가 무엇인지 나아가 그것들이 전체 플라톤 철학과 관련하여 어떤 철학적 함축을 지닌 것인지를 오랫동안 탐문해왔다.(우리나라에서도 주요 해석가들의 연구 성과들을 바탕으로 이러한 상응 관계를 자세하게 비교 분석한 논문이 발표되었다.  강성훈, 「플라톤의 『국가』에서 선분의 비유와 동굴 비유」, 『철학 사상』 V.27, 서울대학교 철학사상연구소, 2008) 그러나 그 세 비유의 영역별 단계별 유사성과 상응 관계에도 불구하고 과연 그 세 비유가 포함하고 있는 영역들이 과연 철학적으로 음미할 만한 정도의 유비적인 상응 관계를 지니는지 끊임없이 논란이 되어 왔을 뿐만 아니라 유사성에 기초한 그 상응 관계에 대한 연구들이 오히려 좋음의 이데아와 관련하여 플라톤이 각 비유를 통해 다각적으로 드러내고자 했던 고유 의도를 간과하게 만드는 것은 아닌지에 대한 우려도 함께 제기되어 왔다. 어쨌거나 플라톤이 세 가지 비유를 든 것은 한 가지 비유만으로는 해소할 수 없는 부분이 있었기 때문이다.

* 세 비유의 영역별 단계별 유사성과 상응 관계에 대해서는 나중 동굴의 비유까지 살핀 후 종합적으로 살펴보겠지만 그것 못지않게 세 비유를 통해 플라톤이 말하고자 한 의도를 제대로 파악하기 위해서는 세 비유 간 차별성과 고유성을 살피는 것 또한 매우 중요하다. 이러한 관점에서 보면, 우선 앞서 살핀 태양의 비유와 선분의 비유만 비교해 보아도 눈에 띄는 구조적 차이점이 발견된다. 그 두 비유는 비록 구조상 동일하게 가시적 영역과 가지적 영역이라는 공통의 구분을 지니고 있지만, 그렇게 두 영역을 구분하는 이유와 배경에는 근본적으로 차이가 있다. 구체적으로 말하자면 태양이 비유에서 가시적인 영역은 가지적인 영역의 인식론적 하위 단계가 아니라 가시적인 영역의 태양으로부터 가지적인 영역의 좋음의 이데아를 유비적으로 추론하기 위해 별도로 상정된 상호 등치적인 영역이다. 다시 말해 전체로는 네 부분이지만 실질적으로는 각 영역별로 분리된 상태에서 동일하게 두 부분 즉 형상의 세계와 믿음의 세계로 구분된다. 그리고 논의 내용 대부분이 기본적으로 태양이 빛을 비추는 대낮의 실물과 눈 그리고 그에 상응하여 좋음의 이데아가 진리와 실재를 비추는 이데아와 영혼에 집중되어 있다. 즉 형상 쪽에 집중되어 있다. 이에 비해 선분의 비유에서 가시적인 영역과 가지적인 영역은 유비관계를 갖는 등치적인 영역이 아니라 인식론적인 위계가 있는 상하 관계를 갖는 비등치적 영역이다. 게다가 두 영역은 위계상 상하 단계로 갖고 있으면서 서로 연속적으로 이어져 있다. 그리고 이곳에서는 지성적 앎의 단계뿐만 아니라 그 하위 단계까지 고르게 다루어지고 있다. 굳이 말하자면 ‘사고’dianoia 단계가 가장 많이 언급되고 있다. 이 점을 고려하면 태양의 비유는 두 영역 간의 유비적 비유를 통해 기본적으로 좋음의 이데아의 근본 특성과 위상을 드러내려는데 기본 목적이 있는 것으로 보인다. 이에 비해 선분의 비유는 그 좋음의 이데아가 속해 있는 지성적 앎의 단계뿐만 아니라 그 하위의 인식론적 단계들까지 자세하게 다루는 방식으로 오히려 하위의 인식 단계들 특히 추론적 사고가 인식의 방법에서 어떻게 형상적 앎과 관계를 지니면서 그 형상적 앎에로 상승하는지를 보여주는데 기본 목적이 있어 보인다.

* 선분의 비유에서 이러한 상승의 측면을 들여다보자면, 가시적 영역의 영상과 실물의 관계는 서로 ‘모상과 원본의 관계’를 가지면서 다시 또 그 실물들은 윗 단계인 가지적인 영역의 ‘사고’의 모상이 된다. 즉 ‘사고’는 영상의 원본인 실물들을 다시 모상들로 이용하여 ‘삼각형 자체’, ‘대각선 자체’를 인식한 후 다시 또 그것을 발판으로 형상에로 다가간다. 즉 각각 단계는 상호 위계 관계를 가지면서 종국적으로 좋음의 이데아가 있는 지성적 앎의 단계로 이어진다. 요컨대 가시적 영역과 가지적 영역은 진리를 향한 연속적인 상승의 과정으로 이어져 있다. 그러니까 삼각형과 대각선을 기준으로 보면 ‘물에 비친 그림자’ 수준(영상eikasia 단계)에서 ‘실제 그려진 삼각형과 대각선’으로 상승하고(확신pistis 단계) 이것들은 사고에 의해 모상들로 이용되면서 ‘삼각형 자체와 대각선 자체’로 상승한다.(사고dianoia) 그리고 마지막으로 변증술적 문답의 능력을 통해 형상적 앎(지성적 앎noēsis)에 이른다. 선분의 비유가 포함하고 있는 이러한 위계적 단계들과 그 단계들이 갖는 인식 방법상의 상승은 나중 동굴의 비유에서 바깥세계를 향해 올라가는 도정anodos의 단계들과 상응되면서 그 철학적 의미에 관한 다양한 해석들이 제기되었다.(이와 관련한 논의는 나중 동굴의 비유에서 다룬다)

* ‘도형’(510b)의 그리스 원어는 ‘형상’의 뜻도 가지고 있는 eidos이다. 그런데 형상은 눈에 보이는 것들이 아니다. 그러므로 여기서 그 말은 eidos의 일상적 용례 그대로 기하학자들이 가정으로 놓고 들어가는 ‘눈에 보이는 그려진 도형들’(510d)을 가리킨다.(<에우튀데모스> 290b 참고) 요컨대 이 단계에서 언급되는 삼각형 자체와 대각선 자체는 마지막 지성적 앎의 단계에서 성립하는 ‘형상’이자 ‘자체적 존재’로서 삼각형 자체, 대각선 자체가 아니다. 그러나 이때 그들이 실제 추론적 사고 과정에서 내내 염두에 두고 있는 것은 눈에 보이는 도형이 아니다. 이를테면 수학 교사나 기하학자들이 칠판에 도형들을 그리며 설명을 할 때 설명을 듣는 사람들은 칠판에 그려진 그림들을 바라보지만 정작 머릿속으로는 그 그림들 배후에 있는 삼각형 자체, 대각선 자체를 떠올리며 그 설명을 이해한다. 그러나 이 추론적 사고 단계에서 성립하는 이러한 삼각형 자체와 대각선 자체는 비록 물질적 성질은 가지고 있지는 않지만, 머릿속 사유 공간에서 연장성을 가지고 존재한다. 연장성은 이차원·삼차원 공간이 갖는 본질적 특성이다. 그러나 형상들이 있는 세계는 그러한 연장성을 탈각해 있다. 즉 형상계는 관계 맺음의 조건으로서 연장성이 성립하지 않는, 말 그대로 형상이 형상 자체로서 존재하는 세계이다. 그러므로 추상적 사고 단계에서 언급되는 삼각형 자체, 대각선 자체는 형상적 자체 존재로서 삼각형 또는 대각선이 아니라 기하학자들이 칠판에 그것을 그리면서 염두에 두고 있는 추상적 도형들로서 비물질적인 삼각형 또는 대각선이다.

* 요컨대 기하학자들은 사고 단계에서 어쩔 수 없이 도형들을 이용하여 삼각형 자체, 대각선 자체라는 앎의 단계에 이르고 그것을 토대로 결론을 내린다. 여기서 ‘결론teleutē을 향해 진행한다’(510b)는 말은 기하학자들이 이를테면 피타고라스의 정리 또는 원의 점점이 하나임을 설명할 때 칠판에 눈에 보이는 도형들을 그려가며 즉 그것을 이용하여 마침내 공리로 증명해내는 것을 말한다. 이처럼 기하학자들이나 계산술 또는 그러한 것들을 하는 사람들은 홀수와 짝수, 도형들과 세 종류의 각기 같은 것들을 따로 설명이 필요 없을 정도로 당연한 것으로 여기고 학술을 수행한다. 플라톤이 추론적 사고와 관련하여 언급하는 ‘가정’hypothesis은 기하학자들이 학술을 수행하면서 이처럼 ‘놓고 들어가는 것들’을 말한다. 그런 점에서 그것은 오늘날 우리가 과학에서 말하는 ‘가설’과 차이가 있다. 이른바 과학에서 말하는 가설은 ‘둘 이상의 변인들 사이의 관계에 관한 일종의 추측 즉, 둘 이상의 변인 또는 현상 간의 관계를 설명하는 검증되지 않은 명제’로서 추후 검증할 수 있도록 기술된 문제에 대한 잠정적인 응답’이다. 그러나 이곳에서 말하는 가정은 명제가 아닌 어떤 존재자들로서, 그 존재자의 실재성에 대한 추측 내지 잠정성이 부재한 상태에서 아무런 검증이나 설명의 필요 없이 분명하고 당연한 존재로서 그냥 말 그대로 ‘놓고 들어가는 존재자들’이다.

* ‘사고’ 단계를 구성하는 학술들 즉 ‘기하학이나 계산술이나 그러한 것들’은 이같이 가정들을 당연한 것으로 여기고 그것들로부터 순수한 연역적 추론에 의해 결론을 이끌어 낸다. 그리고 그 결론들은 이성에 의한 변증술적인 대화(문답) 능력을 통해 첫 원리로 향하는 발판이 되고 종국적으로 일정 단계에 이르면 지성을 통해 형상들에 대한 앎과 그 총체로서 좋음의 이데아에 대한 앎에 이른다. 글라우콘은 소크라테스가 말하는 ‘기하학이나 계산술이나 그러한 것들’을 ‘기하학이나 그와 유사한 전문기술들technai’로 바꾸어 부르는데(511b) 플라톤은 이러한 학술들을 나중 변증술을 설명하는 단계에 가서 변증술의 획득을 위한 예비교과목(521c-531c)에 속하는 학술들로 구체화한다. 수학, 평면 기하학, 입체 기하학, 천문학 및 화성학 등이 그것이다.

* 플라톤은 이제 가지적 영역에서 기하학이나 계산술과 같이 가정을 사용하는 경우를 위와 같이 언급한 후에 가지적인 것의 다른 한쪽 부분 즉 가정을 전혀 사용하지 않는 지성적 앎oēsis에 대해 언급한다.(511b-c) 플라톤은 그것을 ‘이성 자체’auos ho logos가 변증술적 대화의 능력을 통해 파악하는 것으로 언급한다. 즉 이성은 가정들을 ‘첫 원리’가 아니라, 말 그대로 가정들로 삼아 그 가정들을 ‘무가정적인 것’, 즉 ‘모든 것의 첫 원리’에 이르기까지의 출발점이자 디딤 발판 같은 것으로 삼는다. 그런데 눈에 띄는 것은 플라톤 자신 이 단계에서 첫 원리에 이르는 역할의 주체를 ‘이성’logos으로 언급하고 있다는 점이다. 사실 logos는 일반적인 의미에서 설명 또는 추론을 의미하는데 플라톤은 마지막 단계의 앎의 상태를 언급하면서 그 이성이란 표현과 지성적 앎noēsis이라는 표현을 함께 사용하고 있다. 엄격한 의미에서 지성적 앎이 종국적으로 이성이 아니라 지성nous을 통해 완성된다는 점을 고려하면 분명 이성과 지성은 다르다. 그럼에도 플라톤이 이곳에서 이성과 지성을 함께 사용하고 있는 것은 추론적 사고에서부터 지성적 앎에 이르기까지의 과정 자체가 연속적인데다가 그 과정 대부분을 기본적으로 이성이 이끌고 있기 때문이다. 532a에서 ‘이성은 좋은 것 자체를 행해 출발하고 그것을 파악하기 전까지 물러서지 않는다.’고 말하고 있는 것도 그 때문이다. 즉 이성은 가지적 영역 전체에 걸쳐 변증법적 문답의 능력을 통해 가정들을 출발점이자 발판으로 삼아 끊임없이 지성적 앎에로의 상승을 견인하는 중심적인 역할을 맡고 있다.

* 게다가 이성은 ‘첫 원리를 파악하고 나면 다시 거꾸로 첫 원리에 근거를 둔 것들에 의존하면서 그런 식으로 다시 결론 쪽으로 내려간다.katabainē’(511c) 이 말은 기하학자가 지성을 통해 형상을 포착한 후 올라온 방식 그대로 재정립된 사고 단계로 내려갔을 때 그의 사고 과정에서 이성이 어떻게 작용하는지를 보여준다. 이성은 변증술적 대화(문답) 능력을 통해 첫 원리에로의 오름도 담보하지만, 그 첫 원리를 깨달은 후 다시 내려오는 과정에서 전문 학술들의 가정들의 학적 근거를 부여하여 그것을 통해 내리는 결론들에도 전문 학술로서 최소한의 학문적 지위를 갖게 해준다. 그리고 이 과정에서 이성은 감각적인 것은 일체 이용하지 않고 형상들 자체만을 사용해서 형상들에 기초해서 결론을 내린다.(511b-c) 이 결론은 사고 단계에서 가정들을 가지고 내리는 결론과 근본적으로 다른 결론이다. 가정들을 당연한 것으로 여겼던 사고는 오름 과정의 극치에서 지성nous을 통해 형상들에서 연원하는 존재 및 인식 근거를 제공받아 내림의 과정에서 형상에 의존하되 말로 할 수 있는 학적인 앎의 기초를 비로소 갖게 되는 것이다. 요컨대 지성적 앎 없이 사고 단계에서 가정들만을 토대로 다다르는 결론은 설사 연역적 정합성을 갖추고 있을지라도 연역이 의존하는 상위 명제의 진리성을 담보하지 못한다는 점에서 진정한 의미에서 학적인 보편성과 객관성을 가질 수 없지만, 그 모태가 되는 첫 원리에 대한 앎을 통해 가정들의 존재 및 인식 근거가 확보될 경우, 그것들을 통해 다시 재정립된 사고 내지 기하학을 비롯한 전문 학술들은 말과 논리로 성립하는 이론적 학문으로서 비로소 기초적인 학적 보편성과 객관성을 부여받을 수 있는 것이다. 이것은 불가의 돈오점수(頓悟漸修)처럼 생각과 생각의 단계적 상승을 통해 그 극치에서 차원이 다른 반야(般若)의 지혜를 일거에 깨닫고 다시 그 깨달음에 의존하여 깨친 생각들을 보전하고 풀어가며 보시(布施)를 실행하는 것과도 비교될 수 있을 것이다.  동굴의 비유에 가면 이러한 단계들이 실천적 역동성을 갖고 보다 실감나게 그려진다.

————————

* 그런데 이쯤에서 우리는 플라톤에게 심각하게 되돌아 보아할 의문이 있다. 그것은 플라톤이 지금 선분의 비유에서 언급되고 있는 위와 같은 인식론적 위계가 조금 앞서 제5권에서 존재론에 기초해서 플라톤이 상당히 공력을 들여 피력하고 있는 앎과 믿음(의견)과 관련한 원칙적인 위계와 근본적으로 차이가 있다는 점이다. 왜냐하면, 제5권에서는 앎epistēmē과 믿음(의견)doxa이 원천적으로 구분되면서 앎의 형상성이 배타적으로 강조되고 있고 믿음은 ‘있는 것도 아니고 있지 않은 것도 아닌 것’으로 가지적인 영역에 속할 수 없는 것으로 규정되고 있기 때문이다. 그러나 이제 선분에 비유에 와서 플라톤은, 앎의 단계는 제5권 그대로 유지하면서도 그것과 원천적으로 구분되었던 하위 인식 단계에 모종의 단계 즉 ‘사고’dianoia라는 단계를 두어 그것까지도 가지적 영역으로 분류하는 것이다. 도대체 플라톤은 왜 조금 전까지만 해도 가히 상당 분량의 존재론적 논의를 토대로 그토록 강조해온 앎과 믿음(의견)의 원천적 차별성을 접어 둔 채 선분의 비유를 통해 앎의 단계에 미치지 못하는 단계까지 설정하여 그것을 가지적 영역의 범위에 포함토록 하는 것일까? 그것은 제5권에서 피력한 그 자신의 앎에 관한 근본 입장에 수정을 가하는 것일까 아님 추가적인 보완일까? 추가적인 보완이라면 그것을 통해 플라톤이 의도하고자 했던 목적은 무엇일까? 그리고 그것은 전체 플라톤 철학에서 어떤 의미를 갖는 것일까? 다음 강해에서 그에 관한 이러한 물음들에 필자 나름의 답을 제시하면서 선분의 비유에 관한 논의를 마무리하고자 한다. – 끝 –

다음 주제 : C. 철인 통치자의 교육 목표와 교과목(502c-541b)

3. 선분의 비유(509c-513c) – (II)